Question

Show that the elastic force of a spring is a conservative force. Hence write an expression for the potential energy of an elastic stretch of spring.

Answer 1

Hint: The Work on a body is stored as converted to energy. There are two main types of mechanical energy namely, kinetic and potential energy. If the body has no velocity then the work done on it is converted entirely to potential energy. And the work done on a round trip by a conservative force is zero.
Formula Used:
\[W=\int{dW}=\int\limits_{0}^{x}{Fdx}\]
\[SpringForce=kx\]

Complete answer:
A conservative force is a force, the work is done by which is independent of path. And thus, the work done on a round trip by the said force is zero.
To prove that the elastic force is a conservative force let's consider a round trip by a spring where it moves a particle to a distance dl and back.
\[{{W}_{total}}={{W}_{A\to B}}+{{W}_{B\to A}}\]

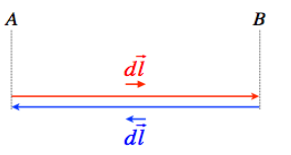
And we know that work done is given by
\[W=\int{dW}=\int\limits_{0}^{x}{Fdx}\]
Now,
\[\begin{align}
  & {{W}_{total}}={{W}_{A\to B}}+{{W}_{B\to A}} \\
 & \Rightarrow {{W}_{total}}=\int\limits_{A}^{B}{F\cdot dl}+\int\limits_{B}^{A}{F\cdot dl} \\
 & \Rightarrow {{W}_{total}}=\int{\left( -kx\widehat{i} \right)\cdot \left( dx\widehat{i} \right)}+\int{\left( -kx\widehat{i} \right)\cdot \left( -dx\widehat{i} \right)} \\
 & \Rightarrow {{W}_{total}}=0 \\
\end{align}\]
As work is done on the round is zero. Therefore, it is proved that elastic force is a conservative force.
For the potential energy of an elastic spring. Let us consider a spring with spring constant k.
Let it be stretched by a very small distance dx. The work done by the spring in this process is dW, and that work is
\[dW=Fdx\]

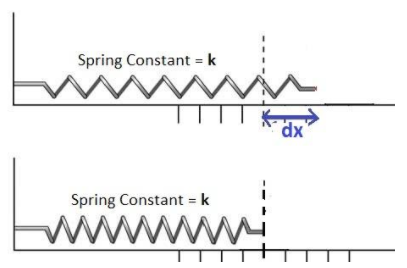
Total work done in stretching the spring from x=0 to x=x will be
\[W=\int{dW}=\int\limits_{0}^{x}{Fdx}\]…...(1)
We also know that the spring force is given by
\[SpringForce=kx\]
And since to stretch we are applying force against it. Therefore, to move the force slowly
\[F=-kx\]
Substituting the value in (1)
\[\begin{align}
  & W=\int{dW}=\int\limits_{0}^{x}{Fdx} \\
 & \Rightarrow W=\int\limits_{0}^{x}{-kxdx} \\
 & \Rightarrow W=-k\int\limits_{0}^{x}{xdx} \\
 & \Rightarrow W=-k\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{x} \\
 & \Rightarrow W=-\dfrac{1}{2}k{{x}^{2}} \\
\end{align}\]
Work Done in moving the spring is \[W=-\dfrac{1}{2}k{{x}^{2}}\]
And since we are moving the spring slowly. There is no kinetic energy. So the entire work done is stored as spring potential energy. Therefore, the expression for spring potential energy is
\[U=-\dfrac{1}{2}k{{x}^{2}}\]

Note:
Forces can be categorised into Conservative and Non-Conservative Forces. The work done by a conservative force is independent of path, that is, the work only depends upon the initial and final state. Meanwhile, for a Non-Conservative Force, the Work Done might also depend upon the path and two cases with the same initial and final positions might have different work done.