Question

Show that the opposite angles of the cyclic quadrilateral are supplementary.

Answer 1

Hint: First, we should construct a cyclic quadrilateral ABCD centred at O and join two lines in the figure as construction as OB and OD. Then, the angle subtended by the minor arc is $\angle x$ and the angle subtended by the major arc is $\angle BOD$. Then, by using the centre angle theorem which states that ‘the central angle is twice the angle on the opposite side of the cyclic quadrilateral’, we get the condition as \[\angle C+\angle A={{180}^{\circ }}\]. Then, by using the angle sum property of the quadrilateral which states that sum of all the angles of the quadrilateral is${{360}^{\circ }}$, we get \[\angle B+\angle D={{180}^{\circ }}\] which proves our condition.

Complete step-by-step answer:
In this question, we prove that the opposite angles of the cyclic quadrilateral is supplementary.
First of all consider a cyclic quadrilateral ABCD centred at O as shown in the figure:

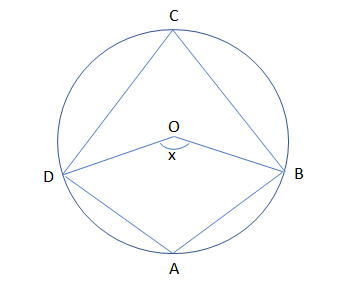
Now, we need to prove that:
$\begin{align}
  & \angle A+\angle C={{180}^{\circ }} \\
 & \angle B+\angle D={{180}^{\circ }} \\
\end{align}$
We have joined two lines in the figure as construction as OB and OD.
Then, the angle subtended by the minor arc is $\angle x$ and the angle subtended by the major arc is $\angle BOD$.
Now, by using the centre angle theorem which states that ‘the central angle is twice the angle on the opposite side of the cyclic quadrilateral’.
So, By using the above mentioned theorem, get two conclusions as:
$\begin{align}
  & \angle x=2\angle C \\
 & \angle BOD=2\angle A \\
\end{align}$
Now by adding the above two expression we get as:
\[\angle x+\angle BOD=2\angle C+2\angle A\]
Then, we know the other property of the cyclic quadrilateral that the summation of both the central angles is ${{360}^{\circ }}$.
So, the equation from this condition becomes as:
 \[\angle x+\angle BOD={{360}^{\circ }}\]
Now by using the above two calculated equations and equating them we get:
\[2\angle C+2\angle A={{360}^{\circ }}\]
Now, solve the above equation to get the expression as:
\[\angle C+\angle A={{180}^{\circ }}\]
This above equation proves the one condition that we require from the cyclic quadrilateral.
Now by using the angle sum property of the quadrilateral which states that the sum of all the angles of the quadrilateral is ${{360}^{\circ }}$.
Now, by applying this property we get:
\[\angle A+\angle B+\angle C+\angle D={{360}^{\circ }}\]
Then, using the above found condition and substituting the value of the angles as \[\angle C+\angle A={{180}^{\circ }}\]:
\[\begin{align}
  & \angle B+\angle D+{{180}^{\circ }}={{360}^{\circ }} \\
 & \Rightarrow \angle B+\angle D={{360}^{\circ }}-{{180}^{\circ }} \\
 & \Rightarrow \angle B+\angle D={{180}^{\circ }} \\
\end{align}\]
So, we get the other condition of the cyclic quadrilateral as \[\angle B+\angle D={{180}^{\circ }}\].
Hence, the opposite angles of the cyclic quadrilateral are supplementary.

Note: For these kinds of questions, we must know the theorem which states the various properties linked to them. Some of the theorems used are the centre angle theorem which states that ‘the central angle is twice the angle on the opposite side of the cyclic quadrilateral’ and other one used in this question is by using the angle sum property of the quadrilateral which states that sum of all the angles of the quadrilateral is ${{360}^{\circ }}$.