Question

Show that the points A (1,2), B (5,4), C (3,8), D (-1,6) are the vertices of a square.

Answer 1

Hint: A square is a quadrilateral whose all four sides are equal and both the diagonals are also equal to each other. We proceed by using distance formula to find the distance between vertice for getting side length and again use for diagonal length between line joining points of diagonal.

Complete step-by-step solution -
To show that the sides are equal and diagonals are equal, we have to find the length of each side and diagonal of the square ABCD.

     

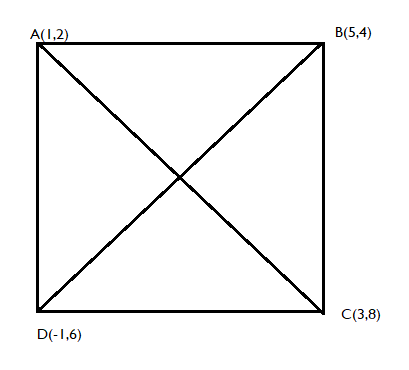
Now, we will find the length by using distance formula. Distance formula is used to find distance between two given points P(${{\text{x}}_1},{{\text{y}}_1}$) and Q (${{\text{x}}_2},{{\text{y}}_2}$). Distance (d) = $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}} $
So, AB = $\sqrt {{{({\text{5 - 1)}}}^2}{\text{ + (4 - 2}}{{\text{)}}^2}} $ = $\sqrt {{4^2}{\text{ + }}{{\text{2}}^2}} $ = $\sqrt {20} $ units
BC = $\sqrt {{{(3{\text{ - 5)}}}^2}{\text{ + (8 - 4}}{{\text{)}}^2}} $ = $\sqrt {{{( - 2)}^2}{\text{ + }}{{\text{4}}^2}} $ = $\sqrt {20} $ units
CD = $\sqrt {{{( - 1{\text{ - 3)}}}^2}{\text{ + (6 - 8}}{{\text{)}}^2}} $ = $\sqrt {{{( - 4{\text{)}}}^2}{\text{ + }}{{\text{2}}^2}} $ = $\sqrt {20} $ units
DA = $\sqrt {{{(1{\text{ + 1)}}}^2}{\text{ + (2 - 6}}{{\text{)}}^2}} $ = $\sqrt {{2^2}{\text{ + ( - 4}}{{\text{)}}^2}} $ = $\sqrt {20} $ units
Now, AC = $\sqrt {{{({\text{3 - 1)}}}^2}{\text{ + (8 - 2}}{{\text{)}}^2}} $ = $\sqrt {{{(2{\text{)}}}^2}{\text{ + (6}}{{\text{)}}^2}} $ = $\sqrt {40} $ units
BD = $\sqrt {{{({\text{ - 1 - 5)}}}^2}{\text{ + (6 - 4}}{{\text{)}}^2}} $ = $\sqrt {{{({\text{ - 6)}}}^2}{\text{ + (2}}{{\text{)}}^2}} $ = $\sqrt {40} $ units
As, we can see that AB = BC = CD = DA and AC = BD. Since, all the sides are equal and both the diagonals are equal to each other, so given points are the vertices of a square.

Note: When we come up with such types of questions, we will prove that the given points are vertices of a quadrilateral with the properties of the given quadrilateral. We will use the distance formula to prove the given statement. Quadrilaterals such as rectangle, square, parallelogram etc, have different properties which will be used to prove the given question. Also, you should apply the distance formula carefully so that there is no mistake when you find the distance as most of the students apply the wrong formula which leads to incorrect answers.