
Show that total energy of a freely falling body remains constant during its motion.
Answer
390k+ views
Hint: When a body falls freely, its kinetic energy increases while its potential energy decreases. But the total mechanical energy is conserved during the free fall.The total mechanical energy of a body at a point during free fall is equal to the sum of kinetic energy and potential energy of the body at that point.
Complete step by step answer:
Consider a body of mass
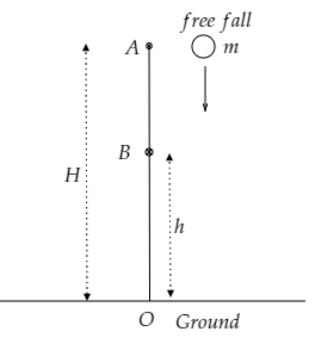
Let the initial height of the body from the ground is
Here,
Therefore,
The potential energy of the body at A is
We know that the total energy of the body is
The total energy of the body at the point B.
Apply the kinematic equation when the body at the point B,
The initial velocity of the body is
The acceleration of the body
The height of the body at B from the ground is
So, the displacement
Therefore,
The kinetic energy at B,
The potential energy at B,
The total energy of the body at point B,
Substitute all the required values in the above formula, we got,
The total energy of the body at the ground.
Similarly, apply the kinematic equation when the body is at the ground point O just before the rest.
The kinetic energy of the body at the ground point O is maximum and is given by
The potential energy of the body at the ground is
The total energy of the body at the ground is,
From above all the three cases, it is found that
Hence, the total energy of a body during free fall is constant.
Note: A body is said to be in free fall motion, when gravity is the only force acting on the body. Therefore, no object has truly free-fall motion due to air friction.Kinetic energy is the energy possessed by a body by virtue of its motion. Potential energy is the energy acquired by a body due to its configuration or change in its position.
Complete step by step answer:
Consider a body of mass

Let the initial height of the body from the ground is
Here,
Therefore,
The potential energy of the body at A is
We know that the total energy of the body is
The total energy of the body at the point B.
Apply the kinematic equation when the body at the point B,
The initial velocity of the body is
The acceleration of the body
The height of the body at B from the ground is
So, the displacement
Therefore,
The kinetic energy at B,
The potential energy at B,
The total energy of the body at point B,
Substitute all the required values in the above formula, we got,
The total energy of the body at the ground.
Similarly, apply the kinematic equation when the body is at the ground point O just before the rest.
The kinetic energy of the body at the ground point O is maximum and is given by
The potential energy of the body at the ground is
The total energy of the body at the ground is,
From above all the three cases, it is found that
Hence, the total energy of a body during free fall is constant.
Note: A body is said to be in free fall motion, when gravity is the only force acting on the body. Therefore, no object has truly free-fall motion due to air friction.Kinetic energy is the energy possessed by a body by virtue of its motion. Potential energy is the energy acquired by a body due to its configuration or change in its position.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
₹ per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




