Answer
355.3k+ views
Hint: We need to find the probability of the six girls sitting together or the boys and girls sitting alternately. Probability of any event is given by the formula $\text{Probability=}\dfrac{\text{Favourable outcomes}}{\text{Total outcomes}}$ . So, we will find the total number of ways in which the boys and girls can be arranged. This will give us our total number of outcomes. Then we will find the number of ways in which six girls sit together. Then we will find the number of ways in which the 6 boys and the 6 girls will sit alternately. Then we will add them both and this gives us our favourable number of outcomes. We will put the values in the above mentioned formula and we will get the required probability.
Complete step by step answer:
Now, we have been given 6 boys and 6 girls and we have to find the probability for the 6 girls to sit together or the boys and girls to sit alternately.
We know that the probability of any event is given by the formula:
$\text{Probability=}\dfrac{\text{Favourable outcomes}}{\text{Total outcomes}}$
Here, favourable outcomes will be the number of ways in which 6 girls can sit together or the boys and girls sit alternately in a row and the total outcomes will be equal to the number of ways in which the 6 boys and 6 girls can sit in a row.
We will first find the number of ways in which the 6 boys and the 6 girls can sit randomly in a row, i.e. the total number of outcomes.
We have 6 boys and 6 girls. Thus, there are a total of $6+6=12$ different people which have to be seated in a row. We know that the number of ways to arrange ‘n’ different objects in a row is given by the formula $n!$ .
Here, we can take 12 different people as the different objects and find out the number of ways in which they can be arranged in a row by putting the value of ‘n’ as ‘12’.
Thus, here $n=12$
Thus, the total number of ways in which 6 boys and 6 girls can be seated in a row is equal to $'12!'$ .
Thus the total number of outcomes is $'12!'$
Now, we will find separately, the number of ways in which 6 girls can sit together and the number of ways in which the 6 boys and 6 girls can sit alternately and add them. Thus, we will get our favourable number of outcomes.
We will now find the number of ways in which the 6 girls can sit together.
Now, for the 6 girls to always sit together, we have to take the group of the 6 girls as one person. Thus, we will now have a total of $6+1=7$ different people which have to be seated in a row.
Now, we know that the total number of ways in which 7 different people can be seated in a row is equal to $'7!'$ .
Now, within the group of the 6 girls, there will be more than one way in which they can be arranged whilst their group is in the same arrangement with the boys.
Now, in the group there are 6 different girls. Thus in the group the arrangement is done in $'6!'$ ways.
As mentioned above, the arrangement in the group of the girls and the arrangement of the group of girls and the boys is done simultaneously. Thus, the number of ways of both these cases will have to be multiplied to obtain the number of ways in which all the girls will always sit together.
Thus, the number of ways in which all the 6 girls sit together is given by:
$\begin{align}
& 7!\times 6! \\
& \Rightarrow 7!6! \\
\end{align}$
Now, we will find the number of ways in which the boys and girls will sit alternately.
For this, let us assume that a girl sits first.
Now, we will use the ‘Gap Method’ to find this. For this, we will fix the position of girls at alternate seats starting from the first seat.
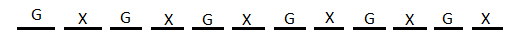
Here, the positions marked as ‘G’ are the positions fixed for the girls and the positions marked as ‘X’ are the positions in which the boys can be seated.
Now, there are a total of 6 positions for 6 boys.
Thus, the number of ways in which the 6 boys can be seated in 6 positions is given by $'6!'$
Now, simultaneously 6 girls have to be seated in 6 positions. The number of ways for doing that is also $'6!'$ .
Thus, the number of ways in which the boys and girls can sit alternately such that a girl sits first is given by:
$\begin{align}
& 6!\times 6! \\
& \Rightarrow 6!6! \\
\end{align}$
Now, if a boy is seated first, there will be an equal number of ways for that alternate arrangement, i.e. $6!6!$ .
Thus, the total number of ways in which the boys and the girls can sit alternately is given as:
$\begin{align}
& 6!6!+6!6! \\
& \Rightarrow 2\times 6!6! \\
\end{align}$
Now, we have found out that the number of ways in which all the girls will sit together is equal to $7!6!$ and the number of ways in which the boys and girls can sit alternately is equal to $2\times 6!6!$
Thus, the number of favourable outcomes is given by:
$\begin{align}
& 7!6!+2\times 6!6! \\
& \Rightarrow \left( 7\times 6! \right)6!+2\times 6!6! \\
& \Rightarrow 6!6!\left( 7+2 \right) \\
& \Rightarrow 9\times 6!6! \\
\end{align}$
Thus, the required probability is given by:
\[\begin{align}
& P=\dfrac{9\times 6!6!}{12!} \\
& \Rightarrow P=\dfrac{9\times 6!6!}{12\times 11\times 10\times 9\times 8\times 7\times 6!} \\
& \Rightarrow P=\dfrac{9\times 6!}{12\times 11\times 10\times 9\times 8\times 7} \\
& \Rightarrow P=\dfrac{9\times 6\times 5\times 4\times 3\times 2\times 1}{12\times 11\times 10\times 9\times 8\times 7} \\
& \Rightarrow P=\dfrac{3}{308} \\
\end{align}\]
Thus, the required probability is equal to $P=\dfrac{3}{308}$
Thus, the option (A) is the correct option.
Note:
Be careful when to multiply the two cases and when to add them. If both the events happen simultaneously then the number of ways in which both of them happen will be multiplied (like when we calculated the number of ways in which all the 6 girls will sit together) and if either of the case is to happen then the number of ways in which they will happen will be added (like we added the number of ways in which 6 girls will always sit together and the number of ways in which the boys and girls will sit alternately).
Complete step by step answer:
Now, we have been given 6 boys and 6 girls and we have to find the probability for the 6 girls to sit together or the boys and girls to sit alternately.
We know that the probability of any event is given by the formula:
$\text{Probability=}\dfrac{\text{Favourable outcomes}}{\text{Total outcomes}}$
Here, favourable outcomes will be the number of ways in which 6 girls can sit together or the boys and girls sit alternately in a row and the total outcomes will be equal to the number of ways in which the 6 boys and 6 girls can sit in a row.
We will first find the number of ways in which the 6 boys and the 6 girls can sit randomly in a row, i.e. the total number of outcomes.
We have 6 boys and 6 girls. Thus, there are a total of $6+6=12$ different people which have to be seated in a row. We know that the number of ways to arrange ‘n’ different objects in a row is given by the formula $n!$ .
Here, we can take 12 different people as the different objects and find out the number of ways in which they can be arranged in a row by putting the value of ‘n’ as ‘12’.
Thus, here $n=12$
Thus, the total number of ways in which 6 boys and 6 girls can be seated in a row is equal to $'12!'$ .
Thus the total number of outcomes is $'12!'$
Now, we will find separately, the number of ways in which 6 girls can sit together and the number of ways in which the 6 boys and 6 girls can sit alternately and add them. Thus, we will get our favourable number of outcomes.
We will now find the number of ways in which the 6 girls can sit together.
Now, for the 6 girls to always sit together, we have to take the group of the 6 girls as one person. Thus, we will now have a total of $6+1=7$ different people which have to be seated in a row.
Now, we know that the total number of ways in which 7 different people can be seated in a row is equal to $'7!'$ .
Now, within the group of the 6 girls, there will be more than one way in which they can be arranged whilst their group is in the same arrangement with the boys.
Now, in the group there are 6 different girls. Thus in the group the arrangement is done in $'6!'$ ways.
As mentioned above, the arrangement in the group of the girls and the arrangement of the group of girls and the boys is done simultaneously. Thus, the number of ways of both these cases will have to be multiplied to obtain the number of ways in which all the girls will always sit together.
Thus, the number of ways in which all the 6 girls sit together is given by:
$\begin{align}
& 7!\times 6! \\
& \Rightarrow 7!6! \\
\end{align}$
Now, we will find the number of ways in which the boys and girls will sit alternately.
For this, let us assume that a girl sits first.
Now, we will use the ‘Gap Method’ to find this. For this, we will fix the position of girls at alternate seats starting from the first seat.
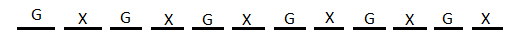
Here, the positions marked as ‘G’ are the positions fixed for the girls and the positions marked as ‘X’ are the positions in which the boys can be seated.
Now, there are a total of 6 positions for 6 boys.
Thus, the number of ways in which the 6 boys can be seated in 6 positions is given by $'6!'$
Now, simultaneously 6 girls have to be seated in 6 positions. The number of ways for doing that is also $'6!'$ .
Thus, the number of ways in which the boys and girls can sit alternately such that a girl sits first is given by:
$\begin{align}
& 6!\times 6! \\
& \Rightarrow 6!6! \\
\end{align}$
Now, if a boy is seated first, there will be an equal number of ways for that alternate arrangement, i.e. $6!6!$ .
Thus, the total number of ways in which the boys and the girls can sit alternately is given as:
$\begin{align}
& 6!6!+6!6! \\
& \Rightarrow 2\times 6!6! \\
\end{align}$
Now, we have found out that the number of ways in which all the girls will sit together is equal to $7!6!$ and the number of ways in which the boys and girls can sit alternately is equal to $2\times 6!6!$
Thus, the number of favourable outcomes is given by:
$\begin{align}
& 7!6!+2\times 6!6! \\
& \Rightarrow \left( 7\times 6! \right)6!+2\times 6!6! \\
& \Rightarrow 6!6!\left( 7+2 \right) \\
& \Rightarrow 9\times 6!6! \\
\end{align}$
Thus, the required probability is given by:
\[\begin{align}
& P=\dfrac{9\times 6!6!}{12!} \\
& \Rightarrow P=\dfrac{9\times 6!6!}{12\times 11\times 10\times 9\times 8\times 7\times 6!} \\
& \Rightarrow P=\dfrac{9\times 6!}{12\times 11\times 10\times 9\times 8\times 7} \\
& \Rightarrow P=\dfrac{9\times 6\times 5\times 4\times 3\times 2\times 1}{12\times 11\times 10\times 9\times 8\times 7} \\
& \Rightarrow P=\dfrac{3}{308} \\
\end{align}\]
Thus, the required probability is equal to $P=\dfrac{3}{308}$
Thus, the option (A) is the correct option.
Note:
Be careful when to multiply the two cases and when to add them. If both the events happen simultaneously then the number of ways in which both of them happen will be multiplied (like when we calculated the number of ways in which all the 6 girls will sit together) and if either of the case is to happen then the number of ways in which they will happen will be added (like we added the number of ways in which 6 girls will always sit together and the number of ways in which the boys and girls will sit alternately).
Recently Updated Pages
Why Are Noble Gases NonReactive class 11 chemistry CBSE

Let X and Y be the sets of all positive divisors of class 11 maths CBSE

Let x and y be 2 real numbers which satisfy the equations class 11 maths CBSE

Let x 4log 2sqrt 9k 1 + 7 and y dfrac132log 2sqrt5 class 11 maths CBSE

Let x22ax+b20 and x22bx+a20 be two equations Then the class 11 maths CBSE

Let x1x2xn be in an AP of x1 + x4 + x9 + x11 + x20-class-11-maths-CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Difference Between Plant Cell and Animal Cell

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE



