
Sketch the graph for $ y = {\tan ^{ - 1}}(\tan x) $
Answer
558k+ views
Hint:
To sketch the graph of $ y = {\tan ^{ - 1}}(\tan x) $ . First, we have to calculate the domain and range of tanx and $ {\tan ^{ - 1}} $ . From this, we can sketch the graph of $ \tan x $ and $ {\tan ^{ - 1}} $ . With the help of these, we can draw a graph of $ y = {\tan ^{ - 1}}(\tan x) $
In a relation R from set A to set B, the set of all first components of order pair belongings to R is called the domain and all the second element of pair is called range.
Complete step by step solution:
We know that the domain of tan. function(tangent function) is the set $ \left\{ {x:x \in R,and.x \ne (2n + 1)\dfrac{\pi }{2},n \in Z} \right\} $
here R represents the real number and $ x \ne (2n + 1)\dfrac{\pi }{2} $ means the domain of tan function does not contain an odd multiple of $ \dfrac{\pi }{2} $ . $ n \in Z $ Represents that n is an integer. Z is the symbol of an integer.
The range of the tan function in R. Here R represents the real number. If we restrict the domain of a tangent function to $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ then it is one-one and onto with the range R. So, the tangent function is restricted to any of interval etc, is bijective and range is R. SO, $ {\tan ^{ - 1}} $ can be defined as the function whose domain is R and range could be any of interval $ \left( {\dfrac{{ - 3\pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right) $ and so on. This interval gives different branches of the function $ {\tan ^{ - 1}} $ . The branch $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ is called the principal value branch of the function $ {\tan ^{ - 1}} $ therefor $ {\tan ^{ - 1}}:R \to \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $
The graph of a tan function $ y = \tan x $ is given as:
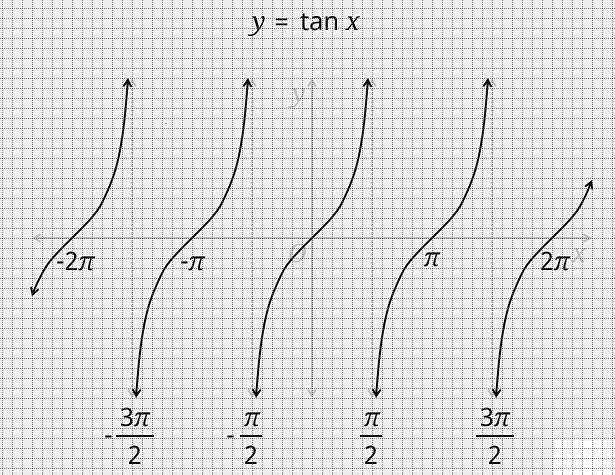
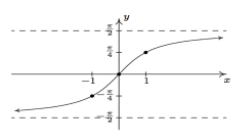
The graph of $ y = {\tan ^{ - 1}}x $ is given as
As $ y = {\tan ^{ - 1}}(\tan x) $ is periodic with period π. therefore to draw this graph we should draw the graph for one interval $ \pi $ and repeat for the entire value.
As we know that $ y = {\tan ^{ - 1}}(\tan x) $ = $ \left\{ {x:\dfrac{\pi }{2} < x < \dfrac{\pi }{2}} \right\} $
This has been defined for $ \dfrac{\pi }{2} < x < \dfrac{\pi }{2} $ that has a length $ \pi $ so its graph could be plotted as

Thus this graph of y where y is not defined for $ x \in (2n + 1)\dfrac{\pi }{2} $ .
Note:
One-one function: A function $ f:x \to y $ is defined as a one-one function of the image of distinct elements of X under $ f $ are distinct.
Onto function: A function is $ f:x \to y $ said to be onto the function of every element of Y is an image of some element of X under f.
Bijective Function: The function which is both one-one and onto is called the bijective function.
To sketch the graph of $ y = {\tan ^{ - 1}}(\tan x) $ . First, we have to calculate the domain and range of tanx and $ {\tan ^{ - 1}} $ . From this, we can sketch the graph of $ \tan x $ and $ {\tan ^{ - 1}} $ . With the help of these, we can draw a graph of $ y = {\tan ^{ - 1}}(\tan x) $
In a relation R from set A to set B, the set of all first components of order pair belongings to R is called the domain and all the second element of pair is called range.
Complete step by step solution:
We know that the domain of tan. function(tangent function) is the set $ \left\{ {x:x \in R,and.x \ne (2n + 1)\dfrac{\pi }{2},n \in Z} \right\} $
here R represents the real number and $ x \ne (2n + 1)\dfrac{\pi }{2} $ means the domain of tan function does not contain an odd multiple of $ \dfrac{\pi }{2} $ . $ n \in Z $ Represents that n is an integer. Z is the symbol of an integer.
The range of the tan function in R. Here R represents the real number. If we restrict the domain of a tangent function to $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ then it is one-one and onto with the range R. So, the tangent function is restricted to any of interval etc, is bijective and range is R. SO, $ {\tan ^{ - 1}} $ can be defined as the function whose domain is R and range could be any of interval $ \left( {\dfrac{{ - 3\pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right) $ and so on. This interval gives different branches of the function $ {\tan ^{ - 1}} $ . The branch $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ is called the principal value branch of the function $ {\tan ^{ - 1}} $ therefor $ {\tan ^{ - 1}}:R \to \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $
The graph of a tan function $ y = \tan x $ is given as:
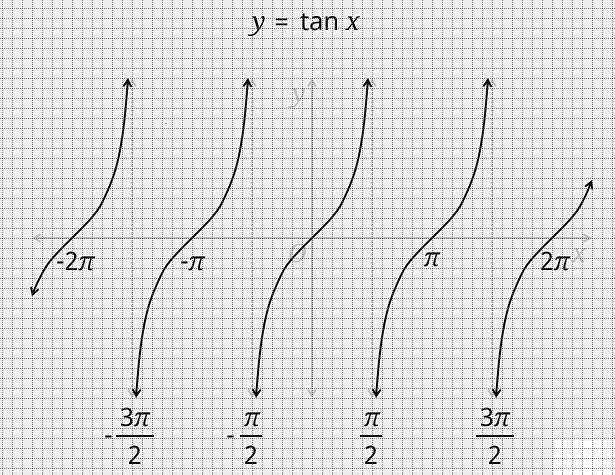
The graph of $ y = {\tan ^{ - 1}}x $ is given as

As $ y = {\tan ^{ - 1}}(\tan x) $ is periodic with period π. therefore to draw this graph we should draw the graph for one interval $ \pi $ and repeat for the entire value.
As we know that $ y = {\tan ^{ - 1}}(\tan x) $ = $ \left\{ {x:\dfrac{\pi }{2} < x < \dfrac{\pi }{2}} \right\} $
This has been defined for $ \dfrac{\pi }{2} < x < \dfrac{\pi }{2} $ that has a length $ \pi $ so its graph could be plotted as

Thus this graph of y where y is not defined for $ x \in (2n + 1)\dfrac{\pi }{2} $ .
Note:
One-one function: A function $ f:x \to y $ is defined as a one-one function of the image of distinct elements of X under $ f $ are distinct.
Onto function: A function is $ f:x \to y $ said to be onto the function of every element of Y is an image of some element of X under f.
Bijective Function: The function which is both one-one and onto is called the bijective function.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




