
What is the slope and intercept for y=9?
Answer
427.5k+ views
Hint: We need to find the slope and intercept of the line y=9. We start to solve the given question by plotting the graph of the line y=9. Then, we find the slope of the given line using the slope formula given by
Complete step-by-step solution:
We are given a line equation and are asked to find the slope of the given line equation. We will be solving the given question using the slope formula
The slope of a straight line is used to determine the steepness of the line. It is usually the ratio of the amount y increases to the amount x increases.
The slope of the line is usually denoted by a variable m.
It is given as follows,
Here,
According to the question,
We need to find the slope of the line y=9.
The graph of the line y=9 is represented as follows,
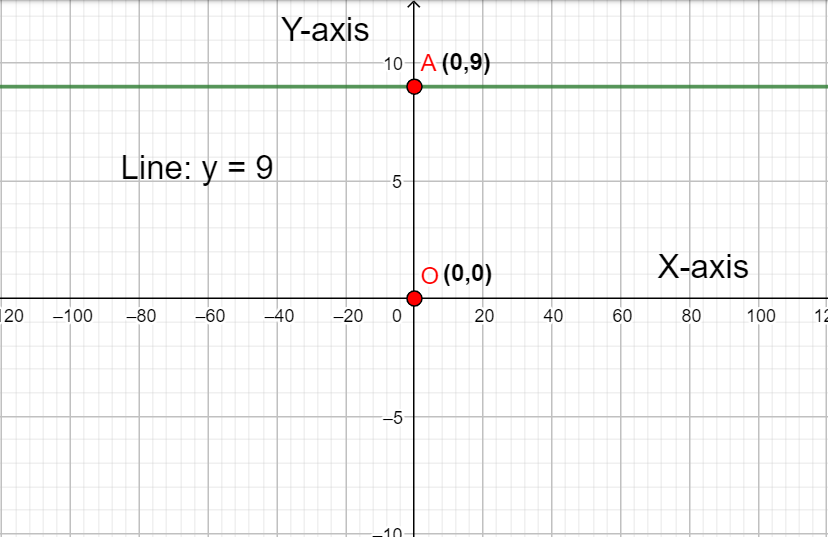
From the graph,
We observe that the line y=9 does not pass through the horizontal axis or the x-axis.
From the above,
The value of y is always equal to 9 for any values of the horizontal coordinates.
Following the same, we get,
Substituting the above values of coordinates in the slope formula, we get,
Simplifying the above equation, we get,
The slope of the line y=9 is zero.
The y-intercept is the point where the graph of the function crosses the y-axis. The point lies on the y-axis.
Hence, the coordinates of the y-intercept are given by
According to our question,
We need to find the value of the y-intercept of the line
From the graph, we know that the graph of the line is crossing the y-axis at the point
So, the coordinates of the y-intercept are given by
Note: The slope of the line can be alternatively found as follows,
The general equation of the straight line is given by
Here,
m = slope
Representing the line y=9 in the form of y=mx+c, we get,
Comparing the above equation with the standard line equation, the slope of the line y=9 is zero.
Complete step-by-step solution:
We are given a line equation and are asked to find the slope of the given line equation. We will be solving the given question using the slope formula
The slope of a straight line is used to determine the steepness of the line. It is usually the ratio of the amount y increases to the amount x increases.
The slope of the line is usually denoted by a variable m.
It is given as follows,
Here,
According to the question,
We need to find the slope of the line y=9.
The graph of the line y=9 is represented as follows,

From the graph,
We observe that the line y=9 does not pass through the horizontal axis or the x-axis.
From the above,
The value of y is always equal to 9 for any values of the horizontal coordinates.
Following the same, we get,
Substituting the above values of coordinates in the slope formula, we get,
Simplifying the above equation, we get,
The slope of the line y=9 is zero.
The y-intercept is the point where the graph of the function crosses the y-axis. The point lies on the y-axis.
Hence, the coordinates of the y-intercept are given by
According to our question,
We need to find the value of the y-intercept of the line
From the graph, we know that the graph of the line is crossing the y-axis at the point
So, the coordinates of the y-intercept are given by
Note: The slope of the line can be alternatively found as follows,
The general equation of the straight line is given by
Here,
m = slope
Representing the line y=9 in the form of y=mx+c, we get,
Comparing the above equation with the standard line equation, the slope of the line y=9 is zero.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




