Question

Slope of a line passing through P(2,3) and intersecting the line, $x+y=7$ at a distance of 4 units from P , is ?
(a) $\dfrac{\sqrt{5}-1}{\sqrt{5}+1}$
(b) $\dfrac{1-\sqrt{5}}{1+\sqrt{5}}$
(c) $\dfrac{1-\sqrt{7}}{1+\sqrt{7}}$
(d) $\dfrac{\sqrt{7}-1}{\sqrt{7}+1}$

Answer 1

Hint: The distance between the point of intersection and point P is 4. The point of intersection lies on the line $x+y=7$ . There will be 2 points on the line $x+y=7$ at a distance of 4 units from the point P. So we will get 2 values of slope.

Complete step-by-step solution:
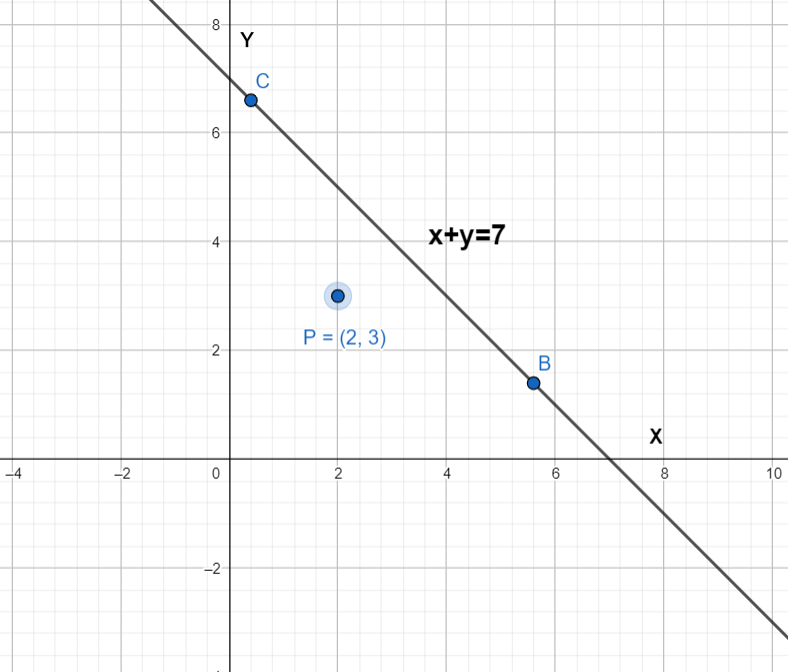
In the above figure point given point P(2,3) has been shown and we have to find the point B and C which are 4 units from P and lies on line $x+y=7$
Then we have to find the slope of lines joining the point PB and PC.
The point of intersection will satisfy the equation of line $x+y=7$ and at a distance of 4 units from P(2,3).
So if we take x coordinate point is $\alpha $the y coordinate will be $7-\alpha $ .So the distance between $\left( \alpha ,7-\alpha \right)$ and P(2,3) is 4 units.
So, by applying distance formula
${{\left( \alpha -2 \right)}^{2}}+{{\left( 4-\alpha \right)}^{2}}=16$
$\Rightarrow $$2{{\alpha }^{2}}-12\alpha +20=16$
$\Rightarrow $${{\alpha }^{2}}-6\alpha +2=0$
By applying the formula $\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ we can find the roots of the equation.
In the equation ${{\alpha }^{2}}-6\alpha +2=0$, a=1,b=-6 and c=2 so substituting these values in the above formula we get
$\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}=$$\dfrac{6\pm \sqrt{{{\left( -6 \right)}^{2}}-4\times 1\times 2}}{2\times 1}$
$\begin{align}
  & \Rightarrow \dfrac{6\pm \sqrt{{{\left( -6 \right)}^{2}}-4\times 1\times 2}}{2\times 1}=\dfrac{6\pm \sqrt{28}}{2} \\
 & \Rightarrow \dfrac{6\pm \sqrt{28}}{2}=\dfrac{6\pm 2\sqrt{7}}{2}=3\pm \sqrt{7} \\
\end{align}$
Roots of the equation are $3+\sqrt{7}$ and $3-\sqrt{7}$
So values of $\alpha $ can be $3+\sqrt{7}$ and $3-\sqrt{7}$. The point of intersection can be $\left( 3+\sqrt{7},4-\sqrt{7} \right)$and$\left( 3-\sqrt{7},4+\sqrt{7} \right)$.
The slope of line joining 2 points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Here in this case the slope of the line joining P and point of intersection will be
$\dfrac{\left( 4-\sqrt{7} \right)-3}{\left( 3+\sqrt{7} \right)-2}=\dfrac{1-\sqrt{7}}{1+\sqrt{7}}$ and $\dfrac{\left( 4+\sqrt{7} \right)-3}{\left( 3-\sqrt{7} \right)-2}=\dfrac{1+\sqrt{7}}{1-\sqrt{7}}$
So the answer will be option C- $\dfrac{1-\sqrt{7}}{1+\sqrt{7}}$.

Note: We can solve this question by other methods. We can assume the slope of the line is m; the point of intersection will be in linear term of m. Then we can apply the distance formula from point P to point of intersection and the equation will be quadratic. So we will get 2 values of m. Another method is we can take the point of intersection $\left( 2+4\cos \theta ,3+4\sin \theta \right)$ where $\tan \theta $ is the slope of line. $\left( 2+4\cos \theta ,3+4\sin \theta \right)$ Will lie on line $x+y=7$.Then we can find the value of $\tan \theta $ .