
How do you solve
Answer
457.8k+ views
Hint: We have been given two linear equations in two variables, variable-x and variable-y which must be solved simultaneously to find the point of intersection of the two given lines. In order to find this point of intersection by the substitution method, we shall substitute the value of variable-y from the second equation to the first equation. After obtaining the value of x-variable, we shall substitute this value in the second equation to calculate the value of y-variable.
Complete step by step answer:
Given that
And
In equation (2), we shall transpose the term with the x-variable to the right hand side and obtain this equation in terms of y-variable which will be further substituted into equation (1).
Substituting this value of y-variable in equation (1), we get
Opening the brackets on the left hand side and multiplying each term by 4, we get
Here, we shall transpose the constant term, 132 to the right hand side and subtract it from 27.
Dividing both sides by 35 to obtain the x-coordinate of the point of intersection, we get
Now, we shall substitute the value of x-variable in equation (2) to obtain the value of y-coordinate.
Transposing the constant term, 24 to the right hand side, we get
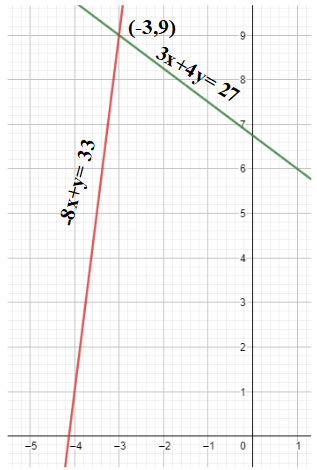
Therefore, the solution or the point of intersection of
Note: Another method of finding the solution or the point of intersection of the given linear equations in two variables was by sketching the graph of both the straight-lines on the same cartesian plane. However, we must take care while marking the points on the graph. The possible mistake which can be made while sketching the graph would be marking (3,0) instead of (-3,0).
Complete step by step answer:
Given that
And
In equation (2), we shall transpose the term with the x-variable to the right hand side and obtain this equation in terms of y-variable which will be further substituted into equation (1).
Substituting this value of y-variable in equation (1), we get
Opening the brackets on the left hand side and multiplying each term by 4, we get
Here, we shall transpose the constant term, 132 to the right hand side and subtract it from 27.
Dividing both sides by 35 to obtain the x-coordinate of the point of intersection, we get
Now, we shall substitute the value of x-variable in equation (2) to obtain the value of y-coordinate.
Transposing the constant term, 24 to the right hand side, we get

Therefore, the solution or the point of intersection of
Note: Another method of finding the solution or the point of intersection of the given linear equations in two variables was by sketching the graph of both the straight-lines on the same cartesian plane. However, we must take care while marking the points on the graph. The possible mistake which can be made while sketching the graph would be marking (3,0) instead of (-3,0).
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Explain the importance of pH in everyday life class 9 chemistry CBSE

On an outline map of India mark the Karakoram range class 9 social science CBSE

What is the N in statistics class 9 maths CBSE

What is the full form of pH?

What is the difference between living and nonliving class 9 biology CBSE

What subjects did Margie and Tommy learn class 9 english CBSE





