Question

How do you solve ${\log _2}\left( {x + 5} \right) - {\log _2}\left( {x - 2} \right) = 3$?

Answer 1

Hint: We have to find all possible values of $x$ satisfying a given equation. Use the property of logarithm function (i) and (ii) to solve the given equation. Then, we will get the solution of the given equation by solving the algebraic equation.
Properties of Logarithm function: Following are some useful properties of logarithm function:
1. ${\log _a}\left( {\dfrac{x}{y}} \right) = {\log _a}\left| x \right| - {\log _a}\left| y \right|$, where $a > 0,a \ne 1$ and $\dfrac{x}{y} > 0$
2. If $x$ and $b$ are positive real numbers and $b \ne 1$, then ${\log _b}\left( x \right) = y$ is equivalent to ${b^y} = x$.

Complete step by step solution:
Given equation: ${\log _2}\left( {x + 5} \right) - {\log _2}\left( {x - 2} \right) = 3$
We have to find all possible values of $x$ satisfying a given equation.
Use the quotient property of logarithms, ${\log _a}\left( {\dfrac{x}{y}} \right) = {\log _a}\left| x \right| - {\log _a}\left| y \right|$.
$ \Rightarrow {\log _2}\left( {\dfrac{{x + 5}}{{x - 2}}} \right) = 3$
Rewrite ${\log _2}\left( {\dfrac{{x + 5}}{{x - 2}}} \right) = 3$ in exponential form using the definition of a logarithm. If $x$ and $b$ are positive real numbers and $b \ne 1$, then ${\log _b}\left( x \right) = y$ is equivalent to ${b^y} = x$.
$ \Rightarrow \dfrac{{x + 5}}{{x - 2}} = {2^3}$
$ \Rightarrow \dfrac{{x + 5}}{{x - 2}} = 8$
Cross multiply the fractions.
$x + 5 = 8\left( {x - 2} \right)$
Apply the distributive property.
$x + 5 = 8x - 16$
Next step is to isolate the variable terms on one side by performing the same mathematical operations on both sides of the equation.
Subtract $8x$ from both sides of the equation, we get
$ - 7x + 5 = - 16$
Next step is to isolate the constant terms on the other side by performing the same mathematical operations on both sides of the equation.
Subtract $5$ from both sides of the equation, we get
$ - 7x = - 21$
Next step is to make the coefficient of the variable equal to $1$ using multiplication or division property.
Divide both sides of the equation by $ - 7$, we get
$x = 3$

Therefore, $x = 3$ is the solution of ${\log _2}\left( {x + 5} \right) - {\log _2}\left( {x - 2} \right) = 3$.

Note: In above question, we can find the solutions of given equation by plotting the equation, ${\log _2}\left( {x + 5} \right) - {\log _2}\left( {x - 2} \right) = 3$ on graph paper and determine all its solutions.

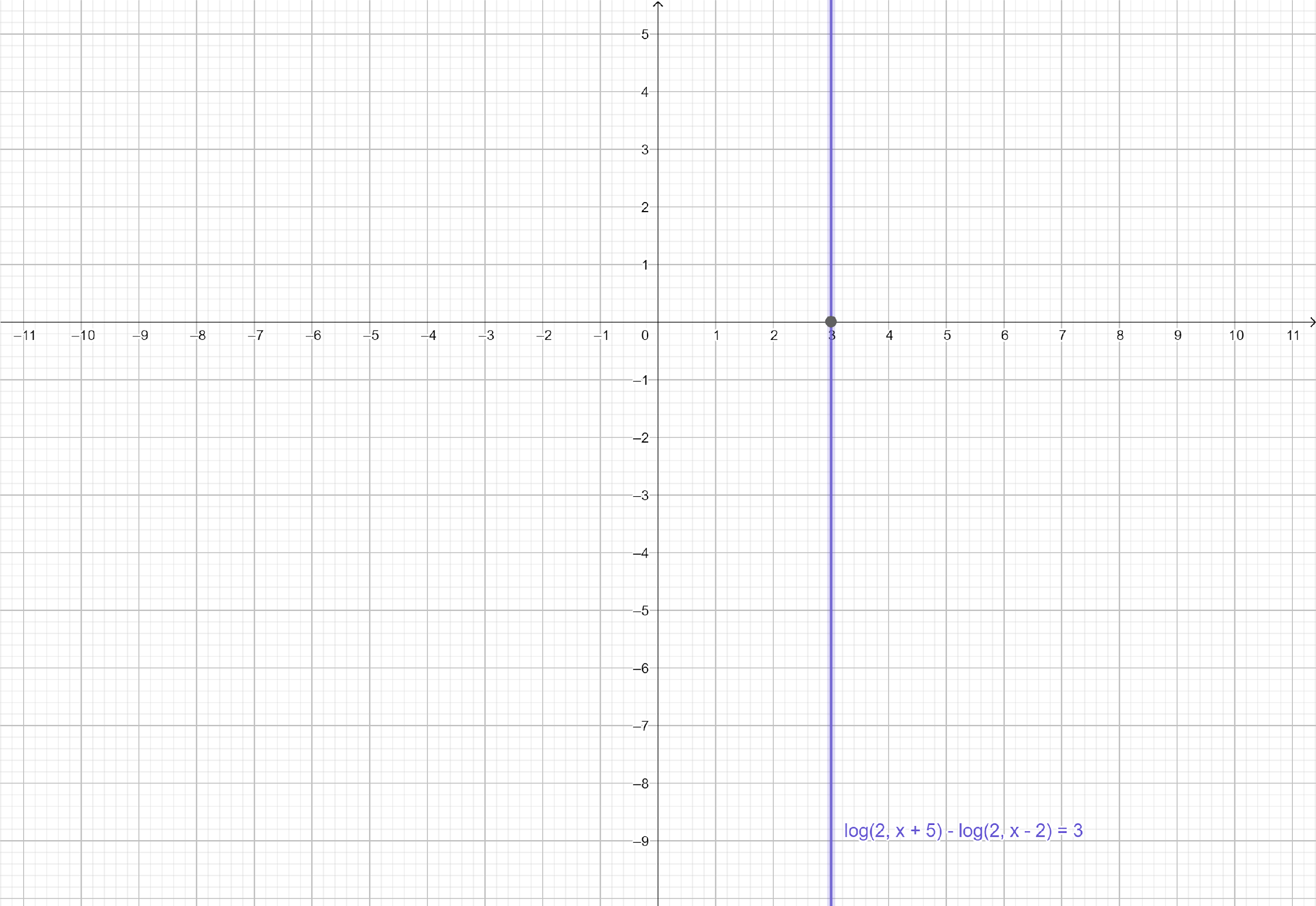
From the graph paper, we can see that $x = 3$ is the only solution of ${\log _2}\left( {x + 5} \right) - {\log _2}\left( {x - 2} \right) = 3$.