Question

Solve the following pair of equations graphically; 2x – 3y = 1 and 4x – 3y + 1 = 0
A. x = 1, y = -1
B. x = -1, y = -1
C. x = -1, y = 1
D. x = 1, y = 1

Answer 1

Hint: Let us plot the given equations in a coordinate plane to get the required value of x and y.

Complete step-by-step answer:
As we are asked to solve the given equations graphically.
So, we had to plot the equation on the graph.
For plotting a linear equation, we need at least 2 points through which the equation passes.
So, for our convenience we find those two points which lie on x-axis and y-axis and also satisfy the equation.
So, as we know that any point lying on the x-axis has y-coordinate equal to zero.
And, any point lying on the y-axis has x-coordinate equal to zero.
Given equations are,
2x – 3y = 1 (1)
4x – 3y + 1 = 0 (2)
So, let equation 1 passes through two points A (a, 0) and B (0, b).
And equation 2 passes through two points C (c, 0) and D (0, d).
Now finding the value of points A, B, C and D to plot them on the graph.
As point A (a, 0) lies on the equation 1. So, it must satisfy equation 1.
2a – 0 = 1
a = \[\dfrac{1}{2}\]
As point B (0, b) lies on the equation 1. So, it must satisfy equation 1.
0 – 3b = 1
b = \[\dfrac{{ - 1}}{3}\]
As point C (c, 0) lies on equation 2. So, it must satisfy equation 2.
4c – 0 + 1 = 0
c = \[\dfrac{{ - 1}}{4}\]
As point D (0, d) lies on equation 2. So, it must satisfy equation 2.
0 – 3d + 1 = 0
d = \[\dfrac{1}{3}\]
Now line joining points A\[\left( {\dfrac{1}{2},{\text{ 0}}} \right)\] and B\[\left( {0,{\text{ }}\dfrac{{ - 1}}{3}} \right)\] will be the equation 2x – 3y = 1.
And the line joining points C\[\left( {\dfrac{{ - 1}}{4},{\text{ 0}}} \right)\] and D\[\left( {0,{\text{ }}\dfrac{1}{3}} \right)\] will be the equation 4x – 3y + 1 = 0.

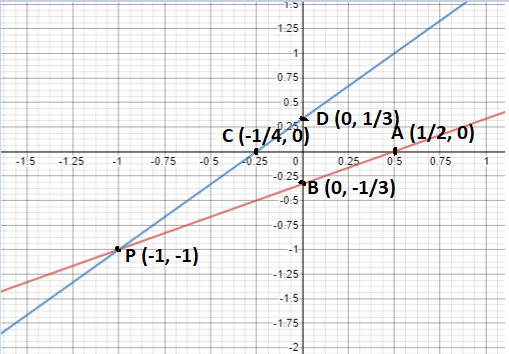
Now we can see from the above graph that both the given lines intersect each other at P (-1, -1).
So, the solution of the given equation will be x = -1, and y = -1.
Hence, the correct answer will be B.

Note: Whenever we come up with this type of problem then to plot any line on a coordinate plane first, we should find points where the equation of line intersects x and y axis. And after plotting those points in the graph we will clearly see the intersection points of all the equations. And this will be the required solution of the problem.