Question

Solve the given magic square and find the values at the missing places.

Answer 1

Hint: In this question, we are given a magic square and are asked to find the values at the missing places. We know that in a magic square, the sum of all elements in each row, each column and each diagonal should be the same. Therefore, we can take a,b,c,d as the variables at the missing places and use the above relation to obtain four linear equations which we can solve to obtain the values of the missing places.

Complete step-by-step answer:
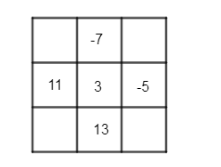
The given magic square is

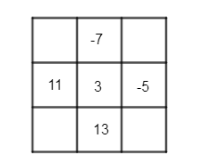
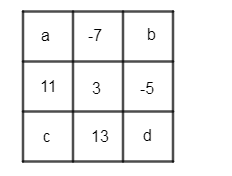
Let us name the missing places as a, b, c and d. We know that in a magic square, the sum of all elements in each row, each column and each diagonal should be the same…………………………(1.1)

The sum of the elements in second row is
 $ 11+3-5=9....................(1.2) $
Using (1.1), and (1.2), we can say that the sum of , the sum of all elements in each row, each column and each diagonal should be equal to 9………………………………..(1.2)
Therefore, from (1.2), as the sum of the first row should be equal to 9, we obtain
 $ \begin{align}
  & a-7+b=9 \\
 & \Rightarrow a+b=9+7=16 \\
 & \Rightarrow b=16-a.......................(1.4) \\
\end{align} $
Also, from (1.2), the sum of the first column should be equal to 9, thus, we obtain
 $ \begin{align}
  & a+11+c=9 \\
 & \Rightarrow a+c=9-11=-2 \\
 & \Rightarrow c=-2-a..........................(1.5) \\
\end{align} $
Again, from (1.2), the sum of the third row should be equal to 9, thus, using this and equation (1.5), we obtain
 $ \begin{align}
  & c+13+d=9 \\
 & \Rightarrow d=9-13-c=-4-(-2-a)=-2+a \\
 & \Rightarrow d=-2+a.....................(1.6) \\
\end{align} $
Also, from (1.2), the sum of the diagonals should be equal to 9, thus, using this and equation (1.6), we obtain
 $ \begin{align}
  & a+3+d=9 \\
 & \Rightarrow a+3+(-2+a)=9 \\
 & \Rightarrow 2a+1=9 \\
 & \Rightarrow a=\dfrac{9-1}{2}=4...............................(1.7) \\
\end{align} $
Now, as we now have the value of a, we can find the values of b, c and d from equations (1.4), (1.5) and (1.6) by putting the value of a from (1.7) as
 $ \begin{align}
  & b=16-a=16-4=12 \\
 & c=-2-a=-2-4=-6 \\
 & d=-2+a=-2+4=2 \\
\end{align} $
Thus, using the above equations, we can fill the magic square as

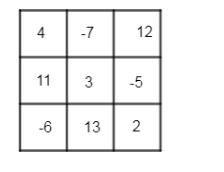
Which is the required answer to this question.

Note: We should note that while solving the equations, we have tried to express b, c and d in terms of a and then use the sum of the diagonals in equation (1.7) to obtain the value of a. However, we can solve the equations by any other method such as elimination, substitution and cross multiplication. However, the answer will still remain the same.