
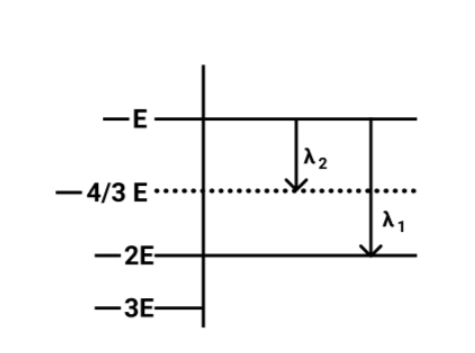
Some energy levels of a molecule are shown in fig. The ratio of the wavelengths $r = {\lambda _1}/{\lambda _2}$is given by:
$\left( a \right)$ $r = \dfrac{1}{3}$
$\left( b \right)$ $r = \dfrac{4}{3}$
$\left( c \right)$ $r = \dfrac{2}{3}$
$\left( d \right)$ $r = \dfrac{3}{4}$
Answer
120k+ views
Hint: we have been given two wavelengths and here are the two transitions. So assuming the corresponding two these two transitions, there is the emission of photons in each case. So firstly we will find the energy of that particular photon then using the relation which we have given in the formula, we will find the ratio between these two wavelengths.
Formula used
The energy of photons,
$E = \dfrac{{hc}}{\lambda }$
Here,
$E$, will be the energy
$h$, will be the planck's constant
$c$, will be the speed of light
$\lambda $, will be the wavelength
Complete Step By Step Solution: As we know the formula for the energy of the photon and it can be written as
$E = \dfrac{{hc}}{\lambda }$
And from here, $\lambda $can be written as
$ \Rightarrow \lambda = \dfrac{{hc}}{E}$
And hence we can say that
$ \Rightarrow \lambda \propto \dfrac{1}{E}$
Now from the figure,
The energy of a photon of wavelength ${\lambda _2}$will be equal to
$ \Rightarrow \vartriangle {E_2} = - E - \left( { - \dfrac{4}{3}} \right)$
On solving the above equation, we get
$ \Rightarrow \vartriangle {E_2} = \dfrac{E}{3}$
Now we will calculate the Energy of the photon of wavelength ${\lambda _1}$ and it will equal to
$ \Rightarrow \vartriangle {E_1} = - E - \left( { - 2E} \right)$
On solving the above equation, we get
$ \Rightarrow \vartriangle {E_1} = E$
So now we will calculate the ratios between the two energies
Therefore, it can be written as
$ \Rightarrow \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{\vartriangle {E_2}}}{{\vartriangle {E_1}}}$
Now on substituting the values, we get
$ \Rightarrow \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{\left( {\dfrac{E}{3}} \right)}}{E}$
So we will solve the final above equation to get the required ratios
$ \Rightarrow r = \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{1}{3}$
Therefore, the option $a$will be the correct choice.
Note: According to Einstein's equation $E = m{c^2}$ anything that possesses energy has mass and anything that has mass has energy which is equal to the mass of the particle times square of the speed of light. Photons have $0$ rest mass but they have Energy which is equal to Planck constant times its frequency. So, if the photon has a fixed amount of energy which will be more than zero with zero rest mass but the photon does not exist which has $0$ moving mass so its energy will be zero.
Formula used
The energy of photons,
$E = \dfrac{{hc}}{\lambda }$
Here,
$E$, will be the energy
$h$, will be the planck's constant
$c$, will be the speed of light
$\lambda $, will be the wavelength
Complete Step By Step Solution: As we know the formula for the energy of the photon and it can be written as
$E = \dfrac{{hc}}{\lambda }$
And from here, $\lambda $can be written as
$ \Rightarrow \lambda = \dfrac{{hc}}{E}$
And hence we can say that
$ \Rightarrow \lambda \propto \dfrac{1}{E}$
Now from the figure,
The energy of a photon of wavelength ${\lambda _2}$will be equal to
$ \Rightarrow \vartriangle {E_2} = - E - \left( { - \dfrac{4}{3}} \right)$
On solving the above equation, we get
$ \Rightarrow \vartriangle {E_2} = \dfrac{E}{3}$
Now we will calculate the Energy of the photon of wavelength ${\lambda _1}$ and it will equal to
$ \Rightarrow \vartriangle {E_1} = - E - \left( { - 2E} \right)$
On solving the above equation, we get
$ \Rightarrow \vartriangle {E_1} = E$
So now we will calculate the ratios between the two energies
Therefore, it can be written as
$ \Rightarrow \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{\vartriangle {E_2}}}{{\vartriangle {E_1}}}$
Now on substituting the values, we get
$ \Rightarrow \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{\left( {\dfrac{E}{3}} \right)}}{E}$
So we will solve the final above equation to get the required ratios
$ \Rightarrow r = \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{1}{3}$
Therefore, the option $a$will be the correct choice.
Note: According to Einstein's equation $E = m{c^2}$ anything that possesses energy has mass and anything that has mass has energy which is equal to the mass of the particle times square of the speed of light. Photons have $0$ rest mass but they have Energy which is equal to Planck constant times its frequency. So, if the photon has a fixed amount of energy which will be more than zero with zero rest mass but the photon does not exist which has $0$ moving mass so its energy will be zero.
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

Trending doubts
Charging and Discharging of Capacitor

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!

Symbol of switch is ON position is class 12 physics JEE_Main

JEE Main 2025 Helpline Numbers for Aspiring Candidates

Electromagnetic Waves Chapter - Physics JEE Main

A combination of five resistors is connected to a cell class 12 physics JEE_Main

Other Pages
JEE Advanced 2024 Syllabus Weightage

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Keys & Solutions

Free Radical Substitution Mechanism of Alkanes for JEE Main 2025

Explain the construction and working of a GeigerMuller class 12 physics JEE_Main

JEE Mains 2025: Exam Dates, Updates, Eligibility and More

Christmas Day 2024 - Origin, History, and Why Do We Celebrate It




