Question

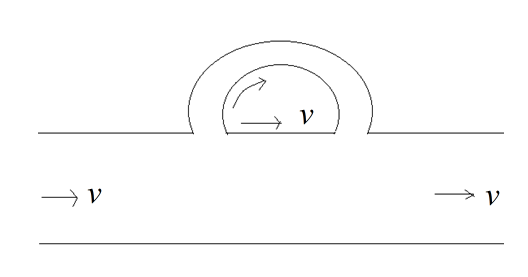
Sound waves are passing through two routes- one in a straight path and the other along a semi-circular path of radius \[r\] and are again combined into one pipe and superposed as shown in figure. If the velocity of sound waves in the pipe is \[v\], then frequency of resultant waves of maximum amplitude will be integral multiples of :

\[\begin{align}
  & A.\dfrac{v}{r(\pi -2)} \\
 & B.\dfrac{v}{r(\pi -1)} \\
 & C.\dfrac{2v}{r(\pi -1)} \\
 & D.\dfrac{v}{r(\pi +2)} \\
\end{align}\]

Answer 1

Hint: If the waves are superimposed and give the maximum amplitude. Then this is the condition of constructive wave form. Therefore we use the condition of constructive wave form which is given by \[\Delta x=n\lambda \].

Formula Used:
For constructive wave form:
Path difference is equal to integral multiple of the wavelength.
\[\Delta x=n\lambda \]

Complete step by step answer:
Sound waves also follow the property of interference.

a.)So when waves are out of phase it has minimum amplitude and we called this a destructive wave. In simple language when two waves cancel out the effect of each other they are called destructive waves.
b.)When waves are in phase, they have maximum amplitude and we call this a constructive wave. In simple language when two waves add the effect of each other they are called constructive waves.

In our question the sound wave travelled from two paths; one path is straight and another path is semi-circular.

Due to this there will be the path difference; because the wave travelling straight reaches first and the wave from the semi- circular path will reach a little bit late. This creates the path difference.

And when these two waves combine they produce maximum amplitude. And therefore this is the case of constructive wave form.

Mathematically,

\[\Delta x=n\lambda \]
Here:
\[\Delta x=\]path difference

\[\Delta x=\]distance wave travelled from semi-circular path minus distance wave travelled from straight path

\[\begin{align}
  & \Delta x=\pi r-2r \\
 & \Delta x=(\pi -2)r \\
\end{align}\]

And we also know that:

\[\Delta x=n\lambda \]

Therefore equating both the equations, we get

\[\begin{align}
  & n\lambda =(\pi -2)r \\
 & n=1 \\
 & \lambda =(\pi -2)r \\
\end{align}\]

Also, we know that there is a relation between velocity of wave, frequency and wavelength.
\[v={{n}^{'}}\lambda \]
Where:

\[{{n}^{'}}=\]frequency of wave
\[v=\] velocity of wave
\[\lambda =\] wavelength of wave
Putting value of wavelength in the above equation, we get the frequency:

\[\begin{align}
  & v={{n}^{'}}(\pi -2)r \\
 & {{n}^{'}}=\dfrac{v}{(\pi -2)r} \\
\end{align}\]
Hence, the correct answer is option A.

Note: Student must remember:
a.)If two waves combines two give maximum amplitude, then this is the case of constructive wave form.
b.)In this question wave is travelling from two paths, so there must be a path difference.