
How do the special right triangles relate to the unit circle?
Answer
465.6k+ views
Hint: From the question given, we have been asked to relate the special right triangles to the unit circle. First of all, we have to know about the special right triangles and unit circle.
There are two types of special right triangles.
Type
Type
In mathematics, a unit circle is a circle of unit radius that is a circle of radius one.
Complete step by step answer:
Now considering from the question we have been asked to relate the special right triangles and unit circle.
From the basic concept we know that there are two types of special right angle triangles.
Type
Type
From the basic concept we know that the Pythagoras theorem states that the square of the longest side that is the hypotenuse is equal to the sum of the squares of the other two adjacent sides in a right angle triangle.
From the below represented figure, we can explain the relation between special right triangles and a unit circle.
Figure:
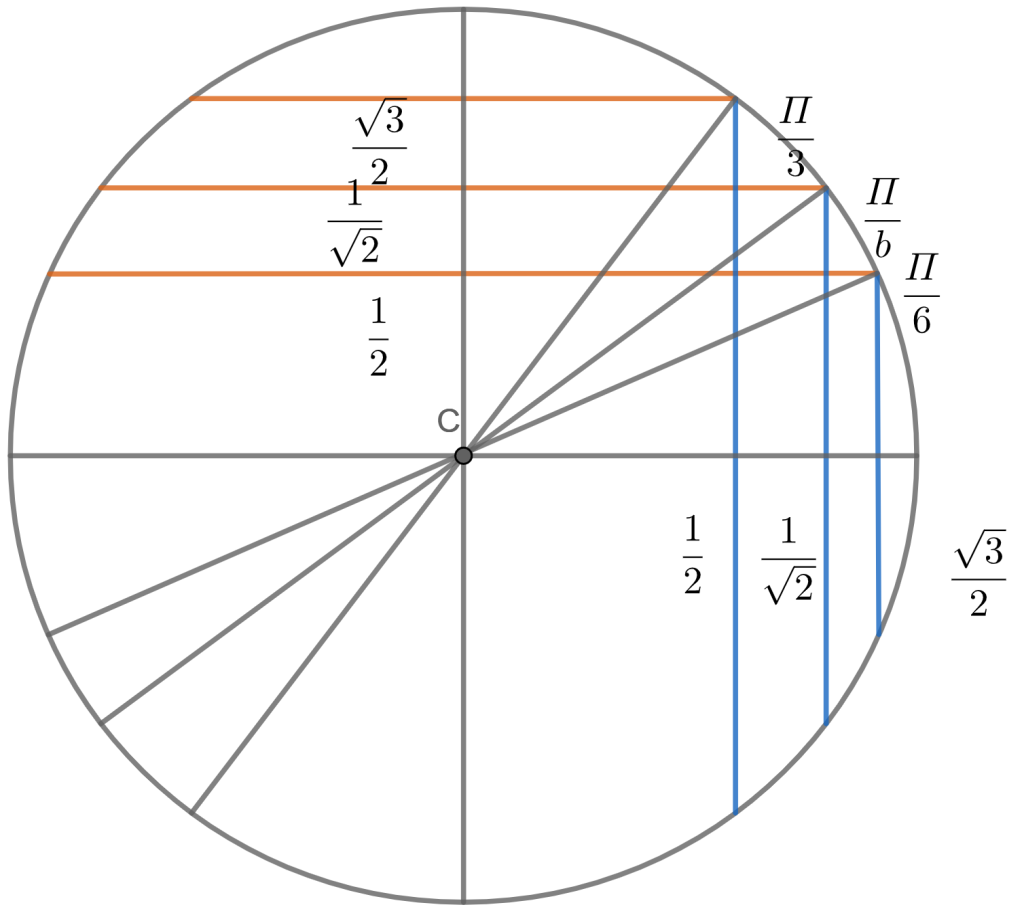
Each black and blue or black and red triangles is a special right angled triangle
The figures outside the circle:
Hence, the special right triangles and the unit circle are related.
Note:
We should be well aware of the concept of special right triangles and unit circles. Also, we should be well known about the relation between special right triangles and unit circles. In this type of question, drawing a figure is the best solution for the question. We should draw the figure according to the question and then have to explain it. Similarly we can do this for any circle.
There are two types of special right triangles.
Type
Type
In mathematics, a unit circle is a circle of unit radius that is a circle of radius one.
Complete step by step answer:
Now considering from the question we have been asked to relate the special right triangles and unit circle.
From the basic concept we know that there are two types of special right angle triangles.
Type
Type
From the basic concept we know that the Pythagoras theorem states that the square of the longest side that is the hypotenuse is equal to the sum of the squares of the other two adjacent sides in a right angle triangle.
From the below represented figure, we can explain the relation between special right triangles and a unit circle.
Figure:

Each black and blue or black and red triangles is a special right angled triangle
The figures outside the circle:
Hence, the special right triangles and the unit circle are related.
Note:
We should be well aware of the concept of special right triangles and unit circles. Also, we should be well known about the relation between special right triangles and unit circles. In this type of question, drawing a figure is the best solution for the question. We should draw the figure according to the question and then have to explain it. Similarly we can do this for any circle.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




