Question

How many spherical lead shots each $4.2cm$ in diameter can be obtained from a rectangular solid of lead with dimensions $66cm,42cm,21cm$ (Use $\pi = \dfrac{{22}}{7}$)

Answer 1

Hint: Here we are given a rectangular lead solid(cuboid) and the lead solid is changed into spherical lead shots, and then we need to find the number of shots that can be made. To find the required answer, we need the formula to find the volume of the cuboid and the volume of the sphere. Also, we need to equate both volumes to obtain the desired answer.

Complete step by step solution:
Here the rectangular lead piece will be in a cuboidal shape.
Hence, the length of the cuboid is $66cm$, the breadth of the cuboid is $42cm$ and the height of the cuboid is $21cm$ .
Also, it is given that the diameter of the sphere is $4.2cm$.
We all know that the radius is half the diameter. Therefore, the required radius of the sphere is $r = \dfrac{{4.2}}{2} = 2.1cm$.
Now, we shall find the volume of the cuboid.
We need to apply the formula Volume of cuboid $ = $ length $ \times $ breadth $ \times $ height
Thus, the volume of the cuboid \[ = 66 \times 42 \times 21c{m^3}\]
Now, we shall find the volume of the sphere.
We shall apply the formula Volume of the sphere \[ = \dfrac{4}{3}\pi {r^3}\]
Thus Volume of the sphere \[ = \dfrac{4}{3} \times \dfrac{{22}}{7} \times {\left( {2.1} \right)^3}\]
$ \Rightarrow \dfrac{4}{3} \times \dfrac{{22}}{7} \times \dfrac{{4.2}}{2} \times \dfrac{{4.2}}{2} \times \dfrac{{4.2}}{2}v$
\[ \Rightarrow 22 \times 0.1 \times 4.2 \times 4.2c{m^3}\]
We are asked to find the number of shots that can be made when the lead solid is changed into lead shots.
Let $n$ be the number of lead shots.
Hence we need to multiply the number of shots with the volume of the sphere and need to compare it with the volume of the cuboid.
That is Volume of $n$ spherical lead shots $ = $ Volume of the cuboid
$ \Rightarrow n \times 22 \times 0.1 \times 4.2 \times 4.2 = 66 \times 42 \times 21$
\[ \Rightarrow n = \dfrac{{66 \times 42 \times 21}}{{22 \times 0.1 \times 4.2 \times 4.2}}\]
\[ \Rightarrow n = \dfrac{6}{{0.2 \times 0.2 \times 0.1}}\]
\[ \Rightarrow n = \dfrac{{6 \times 1000}}{{2 \times 2}}\]
\[ \Rightarrow n = 1.5 \times 1000\]
$ \therefore n = 1500$
Therefore, $1500$ shots can be made.

Note:

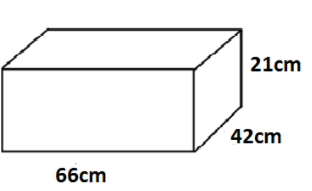
Here, we are given a rectangular lead piece and it is nothing but a cuboid. The dimensions of the cuboid are $66cm,42cm,21cm$. We may get confused to choose the length, breadth, and height from the given $66cm,42cm,21cm$. When we analyze the figure of the cuboid, we are able to note that the length is the largest dimension and height is the smallest dimension.