Question

Split the following shapes into rectangles and find their areas. (The measures are given in centimeters).

Answer 1

Hint: In this question, we are given three figures and we need to find the areas of these figures. For finding the areas of these figures, we will be splitting all these figures into 2 rectangles. Then the area of the respective figure will be equal to the sum of two rectangles. The area of rectangle is given by
$ \Rightarrow Area = l \times b$

Complete step-by-step answer:
In this question, we are given 3 figures and we need to find their areas by splitting them into rectangles.
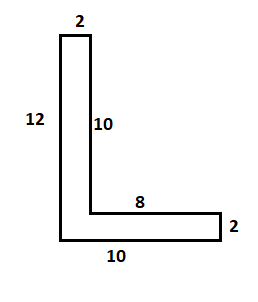
Let us take first figure and find out its area.

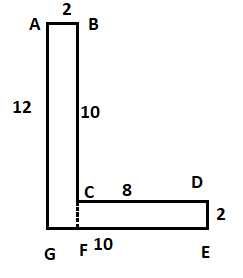
In this figure, we have divided the figure ABCDEG into two rectangles ABFG and rectangle CDEF.
So, the area of the figure ABCDEG will be equal to the area of ABFG plus area of CDEF.
$ \Rightarrow $Area of ABCDEG$ = \square ABFG + \square CDEF$
Now, area of a rectangle is given by length multiplied by breadth. Therefore,

$ \Rightarrow $Area of ABCDEG$ = \square ABFD + \square CDEF$
                                   $ = \left( {AB \times AG} \right) + \left( {CD \times DE} \right)$
Here, we have $AB = 2$, $AG = 12$, $CD = 8$ and $DE = 2$. Therefore,
$ \Rightarrow $Area of ABCDEG$ = \left( {2 \times 12} \right) + \left( {8 \times 2} \right)$
                                   $
   = 24 + 16 \\
   = 40c{m^2} \\
 $
Hence, the area of the first figure ABCDEG is $40c{m^2}$.
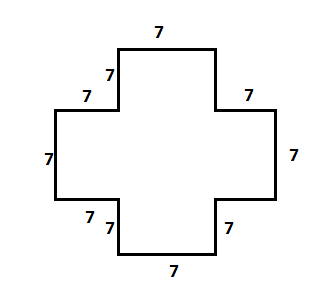
Now, let us take second figure.

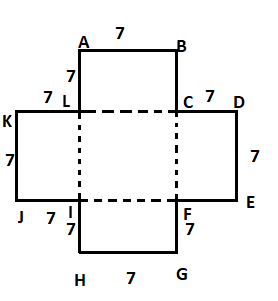
Here, we have divided the figure ABCDEFGHIJKL into two rectangles ABGH and KDEJ.
So the area of the figure ABCDEFGHIJKL will be equal to the sum of areas of rectangles ABGH and KDEJ.
$ \Rightarrow $Area of figure ABCDEFGHIJKL$ = \square ABGH + \square KDEJ$
                                                          $ = \left( {AB \times BG} \right) + \left( {KD \times KJ} \right)$
Here, $AB = 7$ and $KJ = 7$
Now, $BG = BC + CF + FG$ and we can see that $BC = AL = 7$ and $CF = DE = 7$
Therefore,
$ \Rightarrow BG = 7 + 7 + 7 = 21$
And $KD = KL + LC + CD$
Here, $KL = 7$, $LC = AB = 7$ and $CD = 7$. Therefore,
$ \Rightarrow KD = 7 + 7 + 7 = 21$
Therefore,
$ \Rightarrow $Area of figure ABCDEFGHIJKL$ = \left( {7 \times 21} \right) + \left( {7 \times 21} \right)$
                                                          $
   = 147 + 147 \\
   = 294c{m^2} \\
 $
Hence, the area of the figure ABCDEFGHIJKL is $294c{m^2}$.
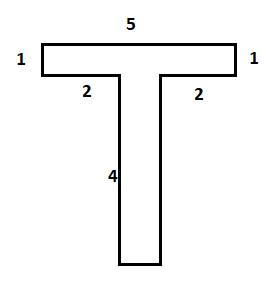
Now, let us take the last figure.

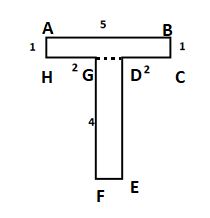
In this figure, we have divided the figure ABCDEFGH into two rectangles ABCH and DEFG.
So, the area of the figure ABCDEFGH will be equal to the sum of areas of rectangles ABCH and DEFG.
$ \Rightarrow $Area of ABCDEFGH$ = \square ABCH + \square DEFG$
                                        $ = \left( {AB \times AH} \right) + \left( {GD \times GF} \right)$
Now, here $AB = 5$ and $AH = 1$ and $GF = 4$.
Now, $GD = AB - FG - DC = 5 - 2 - 2 = 1$. Therefore,
$ \Rightarrow $ Area of ABCDEFGH$ = \left( {5 \times 1} \right) + \left( {1 \times 4} \right)$
                                         $
   = 5 + 4 \\
   = 9c{m^2} \\
 $
Hence, the area of the third figure ABCDEFGH is $9c{m^2}$.

Note: We can also find the areas of this figures by dividing them in different ways.
For example:

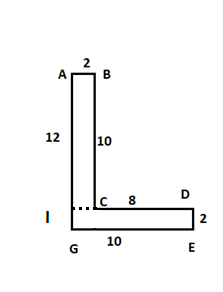
We can also find the area of the first figure in this way.
$ \Rightarrow $Here, the area of figure ABCDEG$ = \square ABCI + \square IDEG$

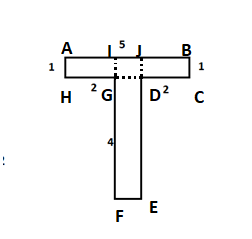
$ \Rightarrow $Here, the area of ABCDEFGH$ = \square IJEF + \square ABCH$