
Split the following shapes into rectangles and find their areas. (The measures are given in centimeters.)
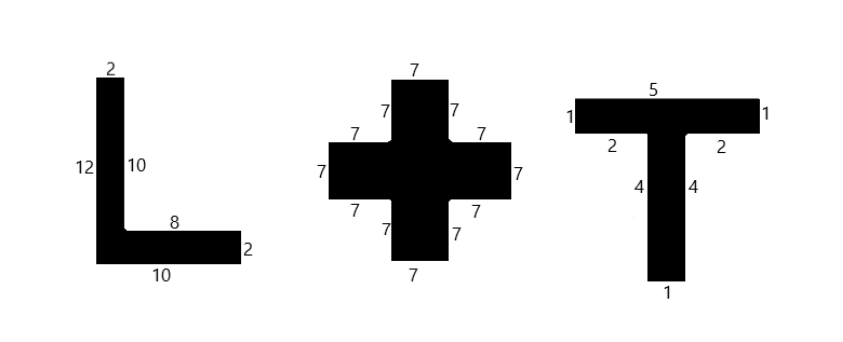

Answer
430.2k+ views
Hint: In this question, we are given three figures, one is of an L, the other is a plus sign and the third is a T. We are given the measurement of each side of the shapes. To find the area of such shapes we don’t have any formula, so we have to divide such figures into different basic figures whose areas can be calculated easily. Then we add all the areas to get the area of the whole shape.
Complete step-by-step answer:
It can be divided into rectangles as follows –
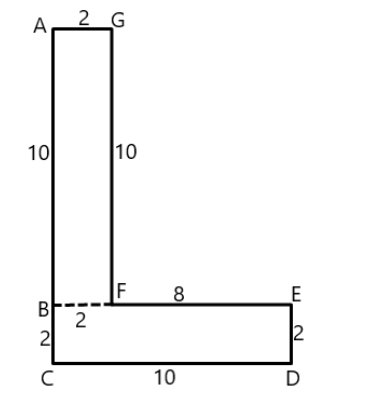
Area of rectangle ABFG
Area of rectangle BCDE
So, the area of the whole shape
This shape can be divided into two rectangles as follows –
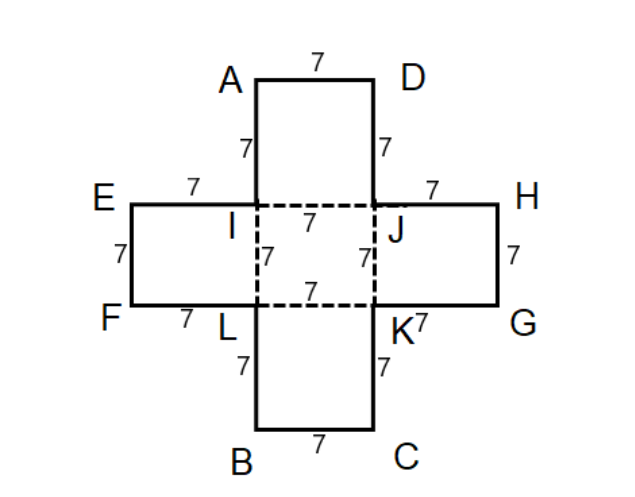
Area of rectangle ABCD
Area of the rectangle EFGH
But the whole will be determined by deleting the middle square part as it has been considered twice. The area of the middle square is
So, Area of the whole shape
This shape can be divided into two rectangles as follows –
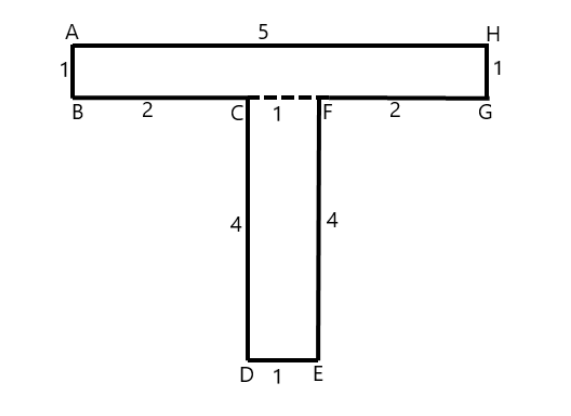
Area of the rectangle ABGH
Area of the rectangle DEFC
Area of the whole shape
Note: We have divided the given shapes into rectangles by using the symmetry and properties of the rectangle. A rectangle is a 4-sided shape in which all the sides are perpendicular to each other and the opposite sides are always equal. A square is a special type of rectangle in which the adjacent sides are also equal. Using these properties we have divided the figure into several parts by the dotted lines.
Complete step-by-step answer:
It can be divided into rectangles as follows –

Area of rectangle ABFG
Area of rectangle BCDE
So, the area of the whole shape
This shape can be divided into two rectangles as follows –

Area of rectangle ABCD
Area of the rectangle EFGH
But the whole will be determined by deleting the middle square part as it has been considered twice. The area of the middle square is
So, Area of the whole shape
This shape can be divided into two rectangles as follows –

Area of the rectangle ABGH
Area of the rectangle DEFC
Area of the whole shape
Note: We have divided the given shapes into rectangles by using the symmetry and properties of the rectangle. A rectangle is a 4-sided shape in which all the sides are perpendicular to each other and the opposite sides are always equal. A square is a special type of rectangle in which the adjacent sides are also equal. Using these properties we have divided the figure into several parts by the dotted lines.
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

10 slogans on organ donation class 8 english CBSE

The LCM and HCF of two rational numbers are equal Then class 8 maths CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE




