Question

Square OABC is drawn with vertex O as origin, vertex A on the positive side of the x−axis and vertex C on the positive side of the y-axis. If each side of the square OABC is of length 6 units, draw OABC on a graph paper and then use the graph to find the coordinates of vertices A, B and C.

Answer 1

Hint: A coordinate graph is a set of two number lines that run perpendicular to one another. These number lines are called axes. The horizontal number line is the x-axis, and the vertical number line is the y-axis. In this question, we draw each point on the graph paper as per condition in the question, and then find the coordinates of the vertices A, B and C.
 Complete step-by-step solution -

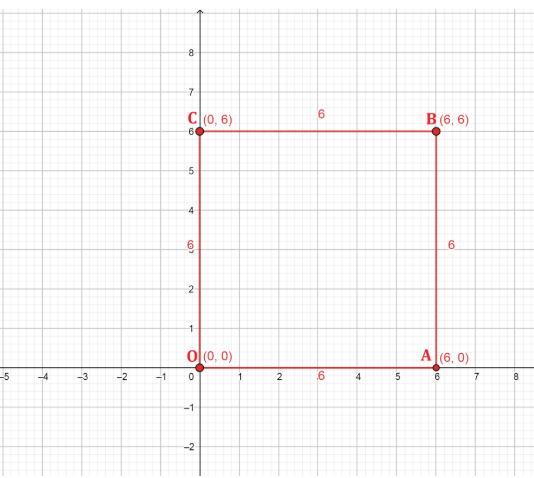
In square OABC as shown in the graph, It is given that the vertex O (0,0) is an origin and as we can see according to the coordinate diagram.

The length of one side of the square is 6 units long in the positive side of X axis and the point indicated by the vertex A.

Also, the length of the second side of the square is also 6 units long in the positive side of the Y axis and the point indicated by the vertex C.

Therefore there is a third vertex that has their x coordinate as 6 and y coordinate is also 6 and which is indicated by the vertex B.

Hence, the value of vertices A and C that are on line with the axis are (6,0) and (0,6) respectively.

For the value of x and y we use the coordinates (6,0) and (0,6), as we can see the value of the x axis is 6 and the value of y is also 6.

Hence the coordinates of the vertex B is (x, y) = (6,6).

Therefore, the coordinates of the vertices A, B and C are (6,0), (6,6) and (0,6).

Note: Note that the ordered pairs are written in parentheses (x-coordinate, y-coordinate) and there is no space after the comma. The two axes intersect where each of them is equal to zero, and this intersection point is called the origin.