Question

State and derive theorem for parallel and perpendicular axes.

Answer 1

Hint
According to the perpendicular axis theorem for an axis perpendicular to the plane, the moment of inertia is equal to the sum of the moments of inertia about 2 mutually perpendicular axes in its own plane. And according to the parallel axis theorem, the moment of inertia about any axis is equal to sum of parallel and passing through the center of mass and product of mass of body and square of distance between the axes.

Complete step by step answer
The parallel axis theorem states that, the moment of inertia of a body about any axis is equal to the moment of inertia about parallel axis through its center of mass plus the product of the mass of the body and the square of the perpendicular distance between the two parallel axes.
Let us consider $I$ is the moment of inertia of a body of mass $M$ about the axis AB. Let us consider another parallel axis CD passing through the center of mass of the body and at a distance $d$ from AB. We consider the moment of inertia about the axis CD of the body as ${I_{CM}}$.

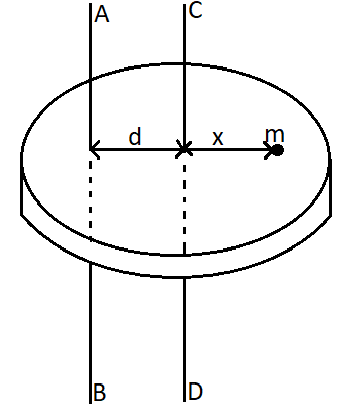
Let us consider a particle of mass $m$ which is at a distance $x$ from the axis CD and at a distance $d + x$ from the axis AB.
So the moment of inertia of this particle about the axis AB is $m{\left( {x + d} \right)^2}$
So to get the moment of inertia about the whole body we use summation. Therefore, we get
$\Rightarrow I = \sum {m{{\left( {x + d} \right)}^2}} $
Now we can break the whole square in the formula as,
$\Rightarrow I = \sum {m\left( {{x^2} + {d^2} + 2xd} \right)} $
So on breaking the individual terms under the summation we get
$\Rightarrow I = \sum {m{x^2} + \sum m {d^2} + \sum {2mxd} } $
Now we can write $\sum {m{x^2}} = {I_{CM}}$
Since the value of $d$ is constant we can bring it outside summation. So we get
$\Rightarrow \sum {m{d^2}} = {d^2}\sum m = M{d^2}$ where $\sum m = M$ is the mass of the whole body.
For the third term, $2d$ comes outside the bracket and since $\sum {mx} = 0$ so the third term vanishes.
Therefore, substituting the values we get
$\Rightarrow I = {I_{CM}} + M{d^2}$.
This is the parallel axis theorem.
The perpendicular axis theorem states that the moment of inertia of a plane lamina about a perpendicular axis is equal to the sum of the moments of inertia of the lamina about any 2 mutually perpendicular axes in its own plane and intersecting each other at the point where the perpendicular axis passes through the lamina.
Let us consider another plane lamina as in the figure.

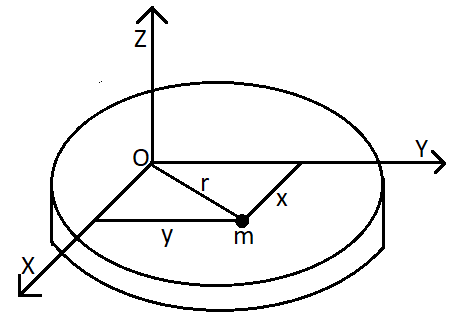
We consider a particle of mass $m$ at the distance $x$, $y$ and $r$ from the X- axis, Y-axis and Z-axis respectively.
Therefore from the figure we can write,
$\Rightarrow {r^2} = {x^2} + {y^2}$
So the moment of inertia of the particle about X-axis is $m{y^2}$
Therefore, for the whole bode, we consider summation and get moment of inertia as,,
$\Rightarrow {I_X} = \sum {m{y^2}} $
Similarly moment of inertia of the whole body about Y-axis is
$\Rightarrow {I_Y} = \sum {m{x^2}} $
And the moment of inertia about Z-axis is
$\Rightarrow {I_Z} = \sum {m{r^2}} $
We can substitute ${r^2} = {x^2} + {y^2}$ and get
$\Rightarrow {I_Z} = \sum {m\left( {{x^2} + {y^2}} \right)} $
On opening the bracket we get
$\Rightarrow {I_Z} = \sum {m{x^2} + \sum m {y^2}} $
We can write this as,
$\Rightarrow {I_Z} = {I_X} + {I_Y}$
This is the perpendicular axes theorem.

Note
The parallel and perpendicular axes theorem are used to find the moment of inertia of various rigid structures about different axes like a rod, disc, sphere, ring, etc. It gives us a simplified way of finding the moment of inertia.