
State and prove basic proportionality theorem.
Answer
477.3k+ views
Hint: The basic proportionality theorem states that “If a line is parallel to one side of a triangle which intersects the other into two distinct points, then the line divides those sides of a triangle in proportion”.
Complete answer:
For a triangle shown below
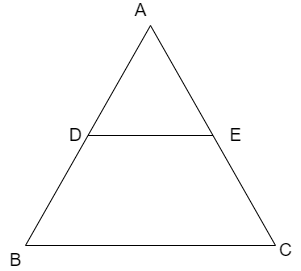
Here, if
We prove this theorem by taking the suitable constructions and using some other standard theorems.
We are asked to state and prove the basic proportionality theorem.
We know that the basic proportionality theorem states that “If a line is parallel to one side of a triangle which intersects the other into two distinct points, then the line divides those sides of a triangle in proportion”.
Now, let us take a triangle
Now, let us join the points B to E and C to D, also let us draw the heights of the triangle
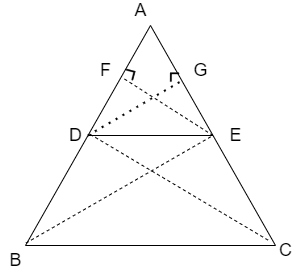
Here, we can see that the line segment EF is height to both triangles
We know that the formula of area of the triangle as
By using the above formula let us find the ratio of area of triangle
Similarly, we can see that the line segment DG is the height of both triangles
By using the area formula of triangle let us find the ratio of area of triangle
Here, we can see that the triangles
We know that the condition that two triangles having the same base and lie between same parallel lines have equal area.
By using the above condition we can say that the area of
Let us divide the both sides with area of triangle
Now, by substituting the required values from equation (i) and equation (ii) in above equation we get
Therefore, we can conclude that the required result has been proved.
That is for a triangle
Note:
We can prove the above result in other method
Here, let us consider the triangles
Here, we can see that all the angles in both triangles
(1)
(2)
(3)
We know that if three angles of two triangles are equal then the two triangles are similar that is
We know that the condition of similar triangles that is the corresponding sides are in proportion.
By using the above condition to triangles
Here, we can see that the sides AB and AC are divided in to two parts.
By rewriting the sides AB and AC as sum of divides parts then we get
Therefore, we can conclude that the required result has been proved.
That is for a triangle
Complete answer:
For a triangle shown below

Here, if
We prove this theorem by taking the suitable constructions and using some other standard theorems.
We are asked to state and prove the basic proportionality theorem.
We know that the basic proportionality theorem states that “If a line is parallel to one side of a triangle which intersects the other into two distinct points, then the line divides those sides of a triangle in proportion”.
Now, let us take a triangle
Now, let us join the points B to E and C to D, also let us draw the heights of the triangle

Here, we can see that the line segment EF is height to both triangles
We know that the formula of area of the triangle as
By using the above formula let us find the ratio of area of triangle
Similarly, we can see that the line segment DG is the height of both triangles
By using the area formula of triangle let us find the ratio of area of triangle
Here, we can see that the triangles
We know that the condition that two triangles having the same base and lie between same parallel lines have equal area.
By using the above condition we can say that the area of
Let us divide the both sides with area of triangle
Now, by substituting the required values from equation (i) and equation (ii) in above equation we get
Therefore, we can conclude that the required result has been proved.
That is for a triangle
Note:
We can prove the above result in other method
Here, let us consider the triangles
Here, we can see that all the angles in both triangles
(1)
(2)
(3)
We know that if three angles of two triangles are equal then the two triangles are similar that is
We know that the condition of similar triangles that is the corresponding sides are in proportion.
By using the above condition to triangles
Here, we can see that the sides AB and AC are divided in to two parts.
By rewriting the sides AB and AC as sum of divides parts then we get
Therefore, we can conclude that the required result has been proved.
That is for a triangle
Recently Updated Pages
Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




