Question

State and prove midpoint theorem.

Answer 1

Hint: According to the midpoint theorem a line through the midpoint of one side of a triangle and parallel to another side, bisects the third side. Draw a line parallel to the side whose midpoint is taken from the point of intersection of the line and the third side. Use congruence rules to prove the theorem.

Complete step-by-step answer:

Statement of midpoint theorem: A line through the midpoint of one side of a triangle, parallel to another side bisects the third side.
Given: A triangle ABC. D is the midpoint of AC. DE||AB.
To prove: E is the midpoint of BC and 2DE = AB
Construction: Draw EF||AC

Proof:

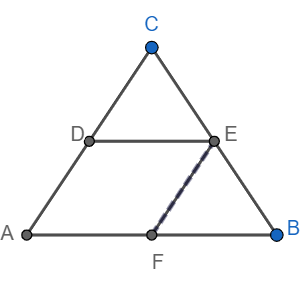
In quadrilateral AFED we have
AD|| FE (By construction)
AF||DE (Given)
Hence AFED is a parallelogram.
Hence AD = EF ...(i)
But since D is the midpoint of AC we have AD = DC ...(ii)
From (i) and (ii) we get
EF = DC
Since AC || EF (by construction) we have
$\angle DCE=\angle FEB$ (corresponding angles)
Also, we have AD||EF
$\Rightarrow \angle CAF=\angle EFB$ (corresponding angles) ...(iii)
Since DE||AB, we have
$\angle CAF=\angle CDE$ (corresponding angles) ...(iv)
From equation (iii) and equation (iv), we get
$\angle CDE=\angle EFB$
Now In $\Delta CDE$ and $\Delta BEF$ we have
CD = FE (proved above)
$\angle CDE=\angle EFB$ (proved above)
$\angle DCE=\angle FEB$(proved above)
Hence $\Delta CDE\cong \Delta EFB$
Hence CE = EB (Corresponding parts of congruent triangles)
Hence E is the midpoint of BC
Also since $\Delta CDE\cong \Delta EFB$
DE = FB (Corresponding parts of congruent triangles) ...(v)
Since, AFED is a parallelogram.
DE = AF ...(vi)
Adding equation (v) and equation (vi), we get
2DE = AF+FB = AB
i.e. DE = AB
Hence proved.
Note: [1] If we join DF, then we divide the triangle into four smaller triangles. It can be shown that all four triangles are congruent to each other. Hence the area of triangle ABC = 4 times area of the triangle DEF
[2] The theorem can also be proved using vector algebra.
Let A (0),\[B\left( \overrightarrow{b} \right)\] and $C\left( \overrightarrow{c} \right)$ be the position vector of each of the points A, B and C.
Now position vector of D $=\dfrac{0+\overrightarrow{c}}{2}=\dfrac{\overrightarrow{c}}{2}$
$\overrightarrow{AB}=P.V\left( B \right)-P.V\left( A \right)=\overrightarrow{b}-0=\overrightarrow{b}$
Hence the equation of DE is
$\overrightarrow{r}=\dfrac{\overrightarrow{c}}{2}+t\overrightarrow{b}$
Equation of BC is \[\overrightarrow{r}=\overrightarrow{b}+u\left( \overrightarrow{b}-\overrightarrow{c} \right)\]
E lies on both the lines DE and BC.
So, we have
\[\begin{align}
  & \overrightarrow{b}+u\left( \overrightarrow{b}-\overrightarrow{c} \right)=\dfrac{\overrightarrow{c}}{2}+t\overrightarrow{b} \\
 & \Rightarrow \left( u+1-t \right)\overrightarrow{b}=\left( \dfrac{1}{2}+u \right)\overrightarrow{c} \\
\end{align}\]
Since \[\overrightarrow{b}\] and \[\overrightarrow{c}\] are Linearly independent, we have
$\begin{align}
  & u+\dfrac{1}{2}=0 \\
 & \Rightarrow u=\dfrac{-1}{2} \\
\end{align}$
and
$\begin{align}
  & u+1-t=0 \\
 & \Rightarrow t=\dfrac{1}{2} \\
\end{align}$
Hence the position vector of E is \[\dfrac{\overrightarrow{c}}{2}+\dfrac{1}{2}\overrightarrow{b}=\dfrac{\overrightarrow{b}+\overrightarrow{c}}{2}\]
which is the midpoint of BC.
Hence E is the midpoint of BC.
Now \[\left| \overrightarrow{DE} \right|=\left| \dfrac{\overrightarrow{c}}{2}-\dfrac{\overrightarrow{b}+\overrightarrow{c}}{2} \right|=\left| \dfrac{\overrightarrow{b}}{2} \right|=\dfrac{1}{2}\left| \overrightarrow{b} \right|=\dfrac{1}{2}\left| \overrightarrow{AB} \right|\]
i.e 2DE = AB
Hence proved.