Question

State and prove the Pythagoras theorem.

Answer 1

Hint: Draw a perpendicular on AC from B and use angle-angle similarity to prove the theorem.

Complete step-by-step answer:
Pythagoras theorem states that “ In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.
The sides of the right-angled triangle are called base, perpendicular and hypotenuse .

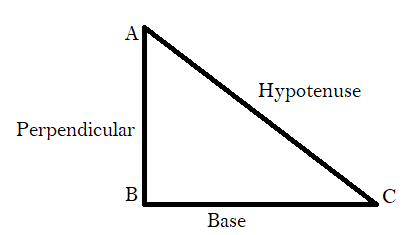
According to Pythagoras theorem ,
${({\text{AC)}}^2} = {({\text{AB)}}^2}{\text{ + (BC}}{{\text{)}}^2}$
Proof:
Given, a triangle ABC in which $\angle {\text{ABC is 9}}{{\text{0}}^0}$.
Construction: Draw a perpendicular BD on AC i.e. BD $ \bot $ AC.

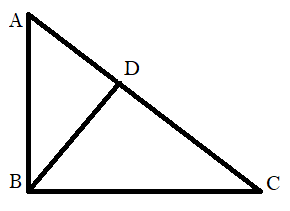
In $\Delta {\text{ABD and }}\Delta {\text{ABC }}$ we have,
$\angle {\text{BAD = }}\angle {\text{BAC }}$i.e. $\angle {\text{A}}$ is common in both triangles.
$\angle {\text{ABC = }}\angle {\text{ADB = 9}}{{\text{0}}^0}$
Therefore $\Delta {\text{ABC}} \sim \Delta {\text{ABD }}$( By AA similarity i.e. angle-angle similarity)
So,$
   \Rightarrow \dfrac{{{\text{AD}}}}{{{\text{AB}}}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}} \\
   \Rightarrow {\text{A}}{{\text{B}}^2}{\text{ = AD}} \times {\text{AC }}...{\text{(1)}} \\
 $
In $\Delta {\text{BDC and }}\Delta {\text{ABC }}$ we have,
$\angle {\text{BCD = }}\angle {\text{BCA }}$i.e. $\angle {\text{C}}$ is common in both triangles.
$\angle {\text{ABC = }}\angle {\text{ADC = 9}}{{\text{0}}^0}$
Therefore $\Delta {\text{ABC}} \sim \Delta {\text{BDC }}$( By AA similarity i.e. angle-angle similarity)
So,$
   \Rightarrow \dfrac{{{\text{DC}}}}{{{\text{BC}}}} = \dfrac{{{\text{BC}}}}{{{\text{AC}}}} \\
   \Rightarrow {\text{B}}{{\text{C}}^2}{\text{ = AC}} \times {\text{DC }}...{\text{(2)}} \\
 $
Adding equation (1) and (2) , we get
$
   \Rightarrow {\text{A}}{{\text{B}}^2}{\text{ + B}}{{\text{C}}^2}{\text{ = AD}} \times {\text{AC + AC}} \times {\text{ DC}} \\
   \Rightarrow {\text{A}}{{\text{B}}^2}{\text{ + B}}{{\text{C}}^2}{\text{ = AC(AD + DC)}} \\
   \Rightarrow {\text{A}}{{\text{B}}^2}{\text{ + B}}{{\text{C}}^2}{\text{ = AC(AC)}} \\
   \Rightarrow {\text{A}}{{\text{B}}^2}{\text{ + B}}{{\text{C}}^2}{\text{ = A}}{{\text{C}}^2} \\
$
Hence, proved.

Note: In a right angled triangle , hypotenuse is the longest side of the triangle and is opposite to the right angle i.e. ${90^0}$. By drawing a perpendicular from point B and dividing the triangle ABC into 2 parts and using angle-angle similarity to prove the Pythagoras theorem.