Question

State BPT theorem and prove it.

Answer 1

Hint: To prove this theorem first we will join BE and CD. Then draw a line EL perpendicular to AB and line DM perpendicular to AC. Now we will find the ratio of area of \[\Delta \]ADE to \[\Delta \]DBE and ratio of area of \[\Delta \]ADE to \[\Delta \]ECD. Comparing the ratios we will get the final answer.

Complete step-by-step answer:
Now, \[\Delta DBE\] and \[\Delta ECD\] being on the same base DE and between the same parallels DE and BC, we have,\[ar(\Delta DBE)=ar(\Delta ECD)\] then we say that the basic proportionality theorem is proved.

Basic proportionality theorem:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
Given:
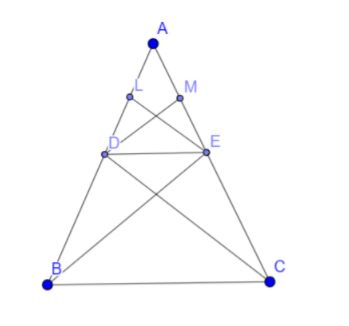
A \[\Delta ABC\]in which \[DE\parallel BC\]and DE intersects AB and AC at D and E respectively.
To prove that:
\[\dfrac{AD}{DB}=\dfrac{AE}{EC}\]
Construction:
Join BE and CD.
Draw \[EL\bot AB\]and \[DM\bot AC\]
Proof:
We have the
\[ar(\Delta ADE)=\dfrac{1}{2}\times AD\times EL\]
\[ar(\Delta DBE)=\dfrac{1}{2}\times DB\times EL\]
Therefore the ratio of these two is \[\dfrac{ar(\Delta ADE)}{ar(\Delta DBE)}=\dfrac{AD}{DB}\]. . . . . . . . . . . . . . (1)
Similarly,
\[ar(\Delta ADE)=ar(\Delta ADE)=\dfrac{1}{2}\times AE\times DM\]
\[ar(\Delta ECD)=\dfrac{1}{2}\times EC\times DM\]
Therefore the ratio of these two is \[\dfrac{ar(\Delta ADE)}{ar(\Delta ECD)}=\dfrac{AE}{EC}\]. . . . . . . . . . . .. . . (2)

Now, \[\Delta DBE\] and \[\Delta ECD\] being on the same base DE and between the same parallels DE and BC, we have,
\[ar(\Delta DBE)=ar(\Delta ECD)\]. . . . . . . . . . . (3)
From equations 1, 2, 3 we can conclude that
\[\dfrac{AD}{DB}=\dfrac{AE}{EC}\]
Hence we can say that the basic proportionality theorem is proved.

Note: The formula for area of the triangle is given by \[\dfrac{1}{2}\times b\times h\]where b, h are base and height respectively. If two triangles are on the same base and between the same parallels then the area of those two triangles are equal.