Question

State Charles law at constant pressure and constant volume.

Answer 1

Hint: The announcement of Charles' law is as per the following: the volume (V) of a given mass of a gas, at the steady weight (P), is straightforwardly relative to its temperature (T).

Complete answer:
Charles' law, or the law of volumes, was found in 1787 by Jacques Charles.
It expresses that, for a given mass of a perfect gas at a consistent weight, the volume is straightforwardly relative to its outright temperature, expecting in a shut framework.
As a numerical condition, Charles' law is composed as either:
\[V\propto T,\]
\[or\,V/T={{k}_{2}}\]
\[or\,{{V}_{1}}/{{T}_{1}}={{V}_{2}}/{{T}_{2}}\]
where the volume of a gas is the supreme temperature and \[{{k}_{2}}\]is a proportionality constant.

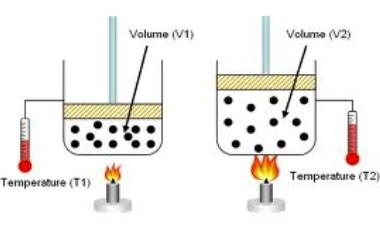
Paul's remark has it right. Charles' Law states "When the weight on an example of a dry gas is held steady, the Kelvin temperature and volume will be legitimately related."
The law says that by the chance that you organize things with the goal that the weight of the gas is fixed then you'll see that \[V\propto T\]. The temperature of the gas may change the weight or the volume, and by and large it's difficult to foresee which will occur.

Note:
We measure the volume of the gas and the temperature of the gas, we have the values \[{{V}_{1\,}}\] and \[{{T}_{1}}\]. Next, begin raising or bringing down the temperature of the gas. The volume should change, thus will the weight, yet once the heat stops again the weight will have returned to its unique worth yet the volume will have changed. Charles' Law says that whenever we do this, we will find that\[\dfrac{{{V}_{2}}}{{{V}_{1}}}=\dfrac{{{T}_{2}}}{{{T}_{1}}}\].