Question

State Hardy- Weinberg principle of Genetic equilibrium. Write any four factors affecting the equilibrium.

Answer 1

Hint: It is the law which helps to calculate the genotype frequencies that will be observed in a population that is not evolving. Human populations do not meet all the conditions of this principle and so it does not follow this.

Complete answer:
The Hardy-Weinberg law or Hardy-Weinberg equilibrium is the fundamental law of population genetics, which provides the idea for studying the Mendelian populations. This law was developed in 1908 by GH Hardy, an English mathematician and G Weinberg, a German physician. The Hardy-Weinberg law states that the genes and genotypic frequencies during a Mendelian population remain constant generation after generation if there's no selection, mutation, migration or random drift.
Thus, factors affecting genetic equilibrium are:
1. Mutations
2. Genetic drift
3. natural selection
4. Gene flow
5. Random mating

Additional Information:
 The law states that in the absence of the disturbing factors the genetic variation of the population from generation to generation remains the constant.
The Hardy-Weinberg equilibrium is often disturbed by a variety of forces, including mutations, survival, nonrandom mating, genetic drift, and gene flow. Similarly, survival and nonrandom mating disrupt the Hardy-Weinberg equilibrium because they end in changes in gene frequencies.
Because all of those disruptive forces commonly occur in nature, the Hardy-Weinberg equilibrium rarely applies actually. Therefore, the Hardy-Weinberg equilibrium describes an idealized state, and genetic variations in nature are often measured as changes from this equilibrium state.

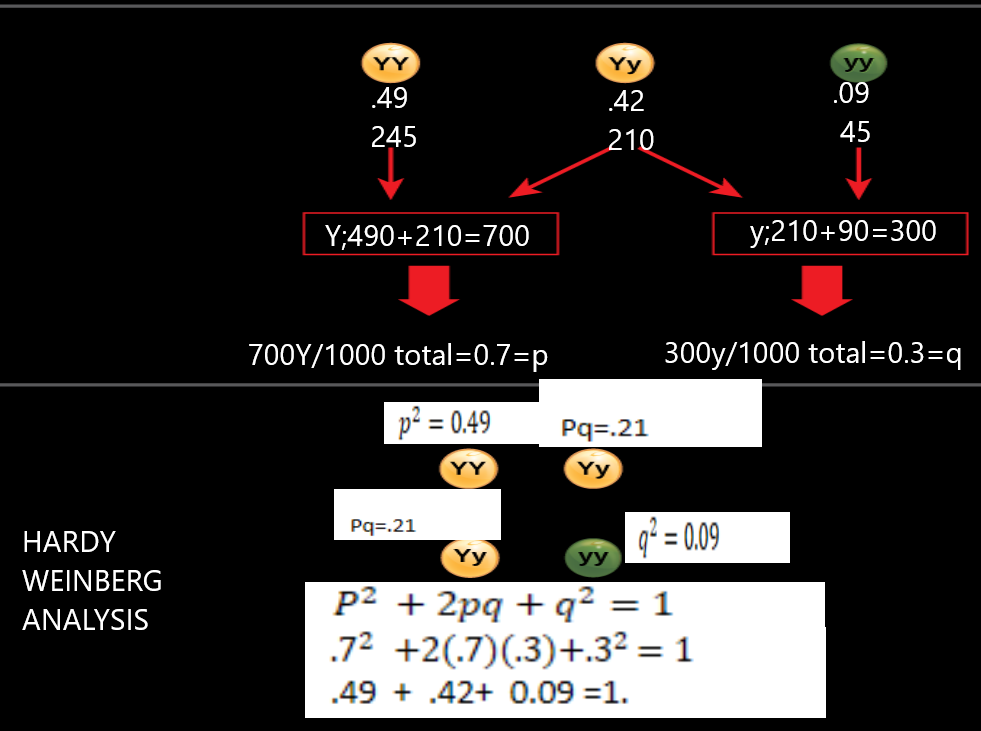
Note: Hardy- Weinberg analysis Equation is: ${ p }^{ 2 }+2pq+{ q }^{ 2 }$
p gives the frequency of the dominant allele and q gives the frequency of the recessive allele. Sum of the frequencies gives 1.
By considering the image below, when we apply this equation, we have;
p=0.7
q=0.3
So, we get,
(0.7)(0.7)+2(0.7)(0.3)+(0.3)(0.3)=1
(0.49)+(0.42)+(0.09)=1
Hence proved.