Question

State Pythagoras theorem and its converse.

Answer 1

Hint: Drop a perpendicular from B to side AC in \[\Delta ABC\] right angled at B and then use similarity of triangles.

Complete step-by-step solution -
Here, we have to state and prove the Pythagoras theorem and its converse. Pythagoras Theorem states that “In a right-angled triangle, the square of hypotenuse side is equal to sum of square of other two sides”
Here, is a right-angled triangle,

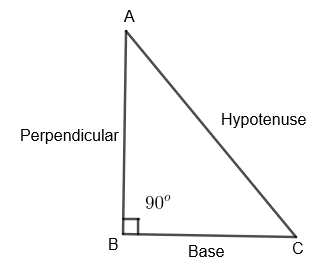
According to Pythagoras Theorem,
\[{{\left( \text{Perpendicular} \right)}^{2}}+{{\left( \text{Base} \right)}^{2}}={{\left( \text{Hypotenuse} \right)}^{2}}\]
\[{{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}\]
Now, to prove Pythagoras theorem, we will take a right- angled triangle ABC.

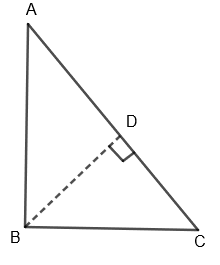
First, we have to drop a perpendicular BD onto the side AC.
Now in \[\Delta ADB\] and \[\Delta ABC\],
\[\angle A=\angle A\]\[\left[ \text{Common Angles} \right]\]
\[\angle BDC=\angle ABC={{90}^{o}}\]
Therefore, \[\Delta ADB\] is similar to \[\Delta ABC\] by Angle-Angle or AA criteria.
Therefore, by condition of similarity that the ratio of corresponding sides are equal.
We get, \[\dfrac{AD}{AB}=\dfrac{AB}{AC}\]
By cross multiplication, we get,
\[A{{B}^{2}}=AD.AC.....\left( i \right)\]
Also, in \[\Delta BDC\] and \[\Delta ABC\]
\[\angle C=\angle C\]\[\left[ \text{Common Angles} \right]\]
\[\angle BDC=\angle ABC={{90}^{o}}\]
Therefore, \[\Delta BDC\] is similar to \[\Delta ABC\] by Angle-Angle or AA criteria.
Therefore, by condition of similarity that the ratio of corresponding sides are equal, we get,
\[\dfrac{CD}{BC}=\dfrac{BC}{AC}\]
By cross multiplication, we get,
\[B{{C}^{2}}=CD.AC....\left( ii \right)\]
By adding equations (i) and (ii), we get,
\[A{{B}^{2}}+B{{C}^{2}}=AD.AC+CD.AC\]
By taking AC common from RHS, we get,
\[A{{B}^{2}}+B{{C}^{2}}=AC\left( AD+CD \right)\]
By diagram, we can see that,
\[AD+CD=AC\]
Therefore we get,
\[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\]
Hence, Pythagoras theorem is proved.
Now, converse of Pythagoras theorem states that “if square of a side is equal to the sum of square of the other two sides then triangle must be right angled triangle”
Now, in converse of Pythagoras Theorem, we are given that if the length of sides of triangle is a, b, c and \[{{c}^{2}}={{a}^{2}}+{{b}^{2}}\], then we have to prove that triangle is right-angled triangle.
As we have already proved the Pythagoras theorem, here we will use its result.

In \[\Delta ABC\], by Pythagoras theorem
\[A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}={{b}^{2}}+{{a}^{2}}.....\left( i \right)\]
Now, to prove the converse of Pythagoras theorem, construct another triangle, \[\Delta EGF\], such that AC = EG = b and BC = FG = a.

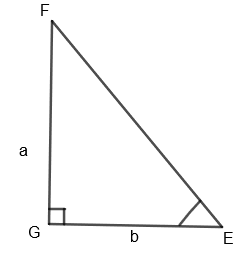
In \[\Delta EGF\], by Pythagoras theorem,
\[E{{F}^{2}}=E{{G}^{2}}+F{{G}^{2}}={{b}^{2}}+{{a}^{2}}.....\left( ii \right)\]
From equation (i) and (ii), we have
\[E{{F}^{2}}=A{{B}^{2}}\]
\[\Rightarrow EF=AB\]
Since, BC = FG = a
\[CA=GE=b\]
And we have proved that AB = EF = c.
Therefore, \[\Delta ACB\] is congruent to \[\Delta EGF\].
Since, we know that in \[\Delta ABC\], C is the right angle.
Therefore, in \[\Delta EFG\], G is also right angled because corresponding parts of congruent triangles are equal.
\[\Rightarrow \angle G\] is right angle
Hence, the converse of Pythagoras theorem is also proved.

Note: Students often make mistakes by assuming AA or AAA criteria as the criteria of congruence of triangles, but it is actually the criteria for similarity of triangles.