Question

State tangent law in magnetism.

Answer 1

Hint: Tangent law is used to determine the strength of two perpendicular magnetic fields. This law is called tangent law because of the tangent factor in the expression. A torque will act on a magnet when it is placed in a magnetic field.

Complete step-by-step answer:

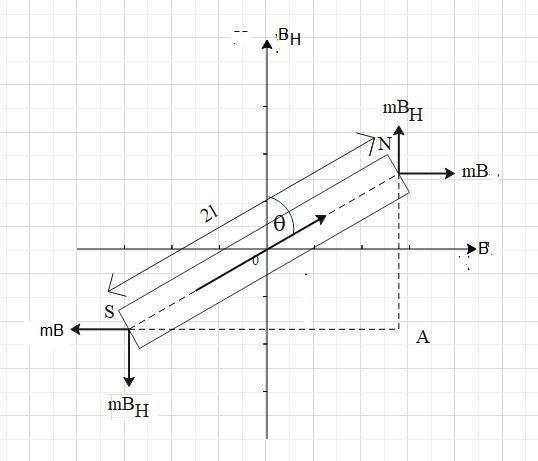
It states that when a magnet is suspended under the action of uniform magnetic fields B perpendicular to the horizontal component of Earth’s magnetic field ,${{B}_{H}}$, then the magnet comes to rest at an angle $\theta $ with respect to the field ${{B}_{H}}$ such that $B={{B}_{H}}\tan \theta $.
Let us suppose a bar magnet suspended in two mutually perpendicular uniform magnetic fields. The magnetic dipole moment M is given as
$\vec{M}=2\vec{l}\times \vec{m}$
Where 2l is the length of magnetic and m is the strength of each pole of the magnet.
When this magnet is placed in the magnetic field a torque acts on the magnet. Thus, when it is placed in a superposition of two magnetic fields then two torques act on the magnet and therefore, the magnet will rotate until it comes in an equilibrium position. At an equilibrium position, two couples balance each other.
Let us draw NA parallel to ${{B}_{H}}$ and SA parallel to B.
The torque acting on magnet due to field ${{B}_{H}}$ is given as
${{\tau }_{1}}=m{{B}_{H}}\times SA$
The torque acting on magnet due to field B is given as
${{\tau }_{2}}=mB\times NA$
The torque ${{\tau }_{1}}$ rotates the magnet in an anticlockwise direction and ${{\tau }_{2}}$ rotates the magnet in the clockwise direction.
At equilibrium,
\[\begin{align}
  & {{\tau }_{1}}={{\tau }_{2}} \\
 & m{{B}_{H}}\times SA=mB\times NA \\
 & \therefore B={{B}_{H}}\times \dfrac{SA}{NA} \\
 & \Rightarrow B={{B}_{H}}\tan \theta \\
\end{align}\]
This proves tangent law.
This angle $\theta $ is known as the angle of dip.

Note: When a magnetic needle is placed in two mutually perpendicular magnetic fields, it will come to the position of rest along the direction of the resultant of the two fields at an angle of $\theta $. When a magnetic needle of a compass is freely suspended in air, it aligns itself along the direction of the horizontal component of the Earth’s magnetic field.