Question

State the following as ‘True’ or ‘False’
The measure of an acute angle $<{{90}^{\circ }}$.
(a) True
(b) False

Answer 1

Hint: To solve this question, we have to recollect the definition of an acute angle.

Complete step-by-step answer:

Before proceeding with this question, we will first discuss the definitions of all types of angles.
In geometry, there are five different types of angles based on their degree measure. These five types of angles are,
1) Acute angle
2) Right angle
3) Obtuse angle
4) Straight angle
5) Reflex angle
Now, we will discuss each of these angles one by one.
1) Acute angle: When we have two lines intersecting each other at angles that are less than ${{90}^{\circ }}$, then we can call that type of angle as an acute angle.

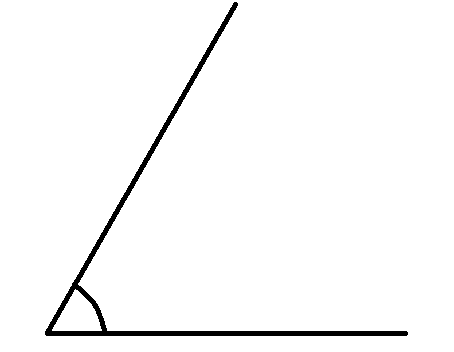
2) Right angle: When we have two lines perpendicular to each other, then we can call that the angle between the two lines as a right angle.

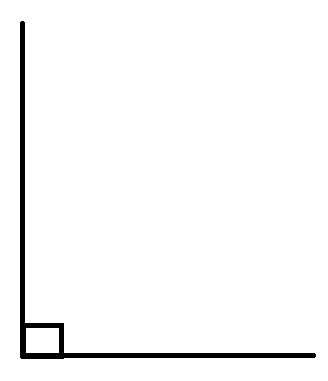
3) Obtuse angle: When we have two lines intersecting each other at angles that are greater than ${{90}^{\circ }}$ and lesser than ${{180}^{\circ}}$, then we can call that type of angle as an obtuse angle.

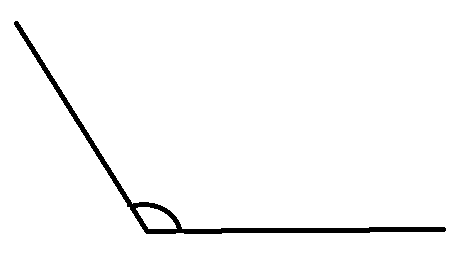
4) Straight angle: When the degree measure of the angle between the two lines is equal to ${{180}^{\circ }}$, we call such an angle a straight angle.

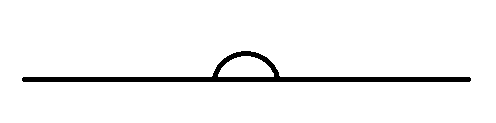
5) Reflex angle: When we have two lines intersecting each other at angles that are greater than ${{180}^{\circ }}$, then we can call that type of angle as a reflex angle.

In the question, the given statement is “the measure of acute angle $<{{90}^{\circ }}$”. From point (1), we know that the angle which has a measure less than ${{90}^{\circ }}$ is called an acute angle.
Hence, the given statement is true.

Note: It is an easy question which can be easily solved with the adequate knowledge of different types of angles. There is a possibility that one may commit a mistake if he/she reads the sign $\left( < \right)$ as $\left( > \right)$ in a hurry to solve this question. So, one must read such types of questions carefully.