Question

State the law of parallelogram of two forces.

Answer 1

Hint:A force is a vector quantity. It has both magnitude and direction. We know parallelogram is an enclosed figure with four sides; opposite sides being parallel and equal to each other. Let us assume that two adjacent sides of a parallelogram represent two forces acting on a point particle and calculate the resultant of the forces.

Complete step by step answer:
The law of parallelogram of two forces states that if two vectors acting on a particle at the same time are represented in magnitude and direction by two adjacent sides of a parallelogram drawn from point their resultant is represented by the diagonal of the parallelogram drawn from the same point.

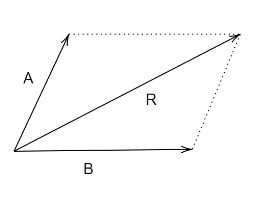
Draw a perpendicular $QR$ to $OR$ produced. And let us assume that $OS = \overrightarrow B $, $QS = OP = \overrightarrow A $ $OQ = \overrightarrow R $and $\angle OPQ = \angle QSR = \theta $

Now considering this if we proceed further, in the case of triangle law of vector addition, the magnitude and direction of resultant vector will be given by
$\left| {\overrightarrow R } \right| = \sqrt {{{\left| {\overrightarrow A } \right|}^2} + {{\left| {\overrightarrow B } \right|}^2} + 2\left| {\overrightarrow A } \right| \bullet \left| {\overrightarrow B } \right|\cos \theta } $

Special cases: -
1.When two vectors are acting in the same direction, then $\theta = 0$and $\cos \theta = 1$.
$\left| {\overrightarrow R } \right| = \sqrt {{A^{^2}} + {B^2} + 2AB} \\
\Rightarrow \left| {\overrightarrow R } \right| = \sqrt {{{(A + B)}^2}} \\
\Rightarrow \left| {\overrightarrow R } \right| = A + B \\ $
Thus, for two vectors acting in the same direction the magnitude of the resultant vector is equal to the sum of the magnitudes of two vectors and act along the direction of $\overrightarrow A $ and $B$.

2. When two vectors are acting in opposite directions, then $\theta = 180$ and $\cos \theta = - 1$.
$\left| {\overrightarrow R } \right| = \sqrt {{A^{^2}} + {B^2} - 2AB} \\
\Rightarrow \left| {\overrightarrow R } \right| = \sqrt {{{(A - B)}^2}} \\
\therefore \left| {\overrightarrow R } \right| = A - B \\ $
Thus, for two vectors acting in opposite directions, the magnitude of the resultant vector is equal to the difference of the magnitudes of the two vectors and acts in the direction of the bigger vector.

Note:It is to be noted that the magnitude of the resultant of two vectors is maximum, when the vectors act in the same direction and is minimum when they act in opposite directions. It should be noted that while finding the resultant vector of two vectors by the parallelogram law of vector addition, the two vectors A and B should either act towards the point or away from the point.