Question

State the number of lines of symmetry of the following figures:
(a)An equilateral triangle
(b)Isosceles triangle
(c)Scalene triangle
(d)Square
(e)Rectangle
(f)Circle

Answer 1

Hint: Think of the basic definition of the line of symmetry and then draw the diagrams of each of the mentioned figures and try to draw their lines of symmetry using the figures and basic properties of the figures.

Complete step-by-step answer:
Before starting with the solution, let us discuss the elements of symmetry and when a body is said to be symmetric or asymmetric. First, we will discuss the two major elements of symmetry, which are the line of symmetry and axis of symmetry.
The "Line of Symmetry" is the imaginary line through the body, which divides the body into two equal halves such that the parts on each side of the body are the mirror images of each other. While the axis of symmetry is an axis passing through the body about which the rotation of the body gives the exact identical figure as the initial one, provided the angle of rotation is less than , and the number of times the figure is repeated while rotating it by is the order of the rotational symmetry.
If a body consists of at least one of the elements of symmetry mentioned above is said to be symmetric. We can represent this diagrammatically as:

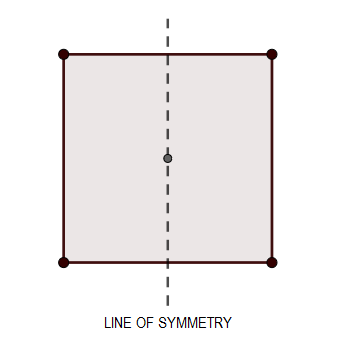
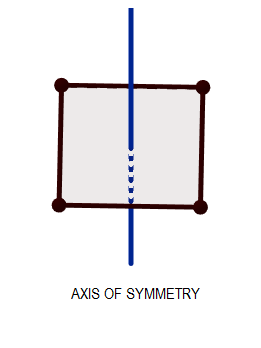
Now let us start the solution to the above question by drawing the diagram of the situations given in the question. First, let us start with the equilateral triangle.

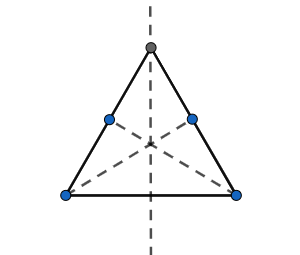
From the figure we can clearly see that the equilateral triangle will have three lines of symmetry.
Now, if we talk about the isosceles triangle, we know that only 2 of its sides are equal. So, unlike the equilateral triangle we would have only 1 line of symmetry passing through the vertex formed by the meeting of the two of its equal sides.

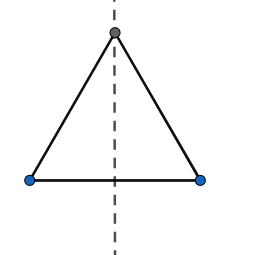
Now, as the scalene triangle has no equal sides, so it is right to say that it is completely asymmetric, so it has no line of symmetry.
Now, as we have finished with the discussion about the triangles, now we will move to the discussion about the specific types of quadrilaterals. We will start with squares. Square is a quadrilateral with all sides equal and opposite sides parallel. So, let us try to figure out the number of lines of symmetry that a square can have.

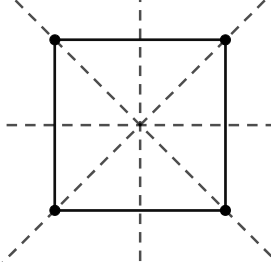
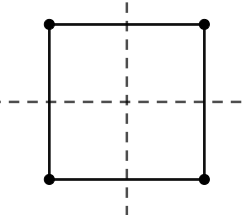
So, the number of lines of symmetry of a square is 4. Rectangle being different from a square has only the opposite sides equal. So, the rectangle would have only two lines of symmetry, as the diagonals would not act like its line of symmetry.

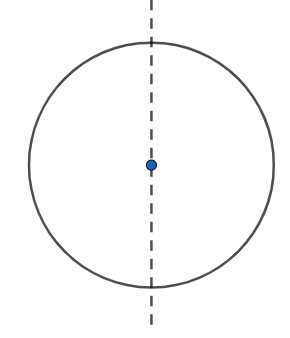
Now for a circle, we know, a circle has an infinite number of lines of symmetry and one axis of rotational symmetry with infinite order of rotational symmetry.

Note: It is better if you learn the number of lines of symmetry for the standard geometrical figure, as it might not be possible every time to draw and find out due to lack of time or proper tools for constructions. Also, in making lines of symmetry manually, you might miss some of the lines of symmetry.