Question

State true or false if a man standing on a platform $3\;{\text{m}}$above from the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.

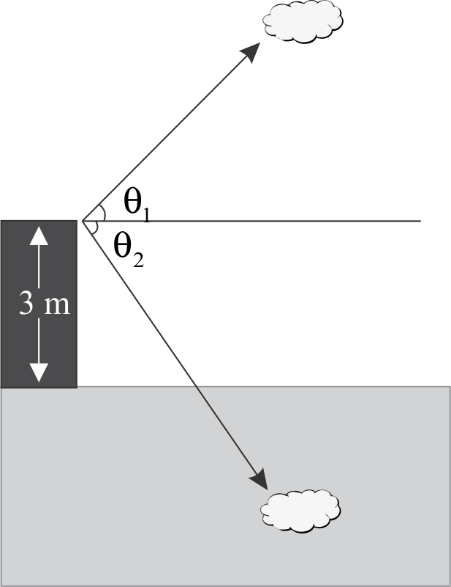
Answer 1

Hint: In this question use the concept of the tangent that is, it is the ratio of the length of the perpendicular to the length of the base. Then compare the tangent of angle ${\theta _1}$ and ${\theta _2}$ to find whether the given statement is true or false.

Complete step-by-step answer:
As per the given statement, let us assume a man standing on a platform at a point A and let C be the point above the surface of a lake observes a cloud.
Let us, consider the following diagram which shows two triangles that is triangle $BAD$ and triangle $CAB$,

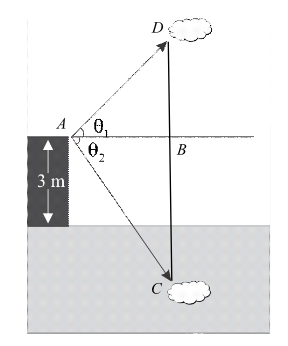
Let the height of the cloud from the surface of the platform is $h$ and the angle of elevation of the cloud is ${\theta _1}$.
Now, at the same point the man observes cloud reflection in the lake at this the height is
$h + 3$ because in the lake the platform height is also added.
In triangle $BAD$,
$
  \tan {\theta _1} = \dfrac{{BD}}{{AB}} \\
  \tan {\theta _1} = \dfrac{h}{{AB}} \\
  \dfrac{{\tan {\theta _1}}}{h} = \dfrac{1}{{AB}} \cdot \cdot \cdot \cdot \cdot \cdot (1) \\
 $
In triangle $CAB$,
$
  \tan {\theta _2} = \dfrac{{CB}}{{AB}} \\
  \tan {\theta _2} = \dfrac{{h + 3}}{{AB}} \\
  \dfrac{{\tan {\theta _2}}}{{h + 3}} = \dfrac{1}{{AB}} \cdot \cdot \cdot \cdot \cdot \cdot (2) \\
 $
Now, on comparing above equations,
$
  \dfrac{{\tan {\theta _1}}}{h} = \dfrac{{\tan {\theta _2}}}{{h + 3}} \\
  \tan {\theta _2} = \left( {\dfrac{{h + 3}}{h}} \right)\tan {\theta _1} \\
 $
Therefore, ${\theta _1} \ne {\theta _2}$. Hence, if a man standing on a platform $3\;{\text{m}}$ above from the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is not equal to the angle of depression of its reflection. Thus, the given statement is false.

Note: We know that calculus and algebra are based on trigonometry. It is widely used in creation of maps and to calculate heights. It is also used in many fields such as architecture, to make designs. In physics and mathematics, it is used to find the components of vectors