Answer
Verified475.2k+ views
Hint: Use the property that the opposite sides of the rectangles are parallel and equal. Then apply the ASA congruence criteria in order to check that the diagonals of a rectangle bisect each other or not.
Complete step-by-step answer:
In the question, we have to check if the statement which says that the diagonals of a rectangle bisects each other is true or not. So here we will first draw the rectangle and the diagonals as shown below:
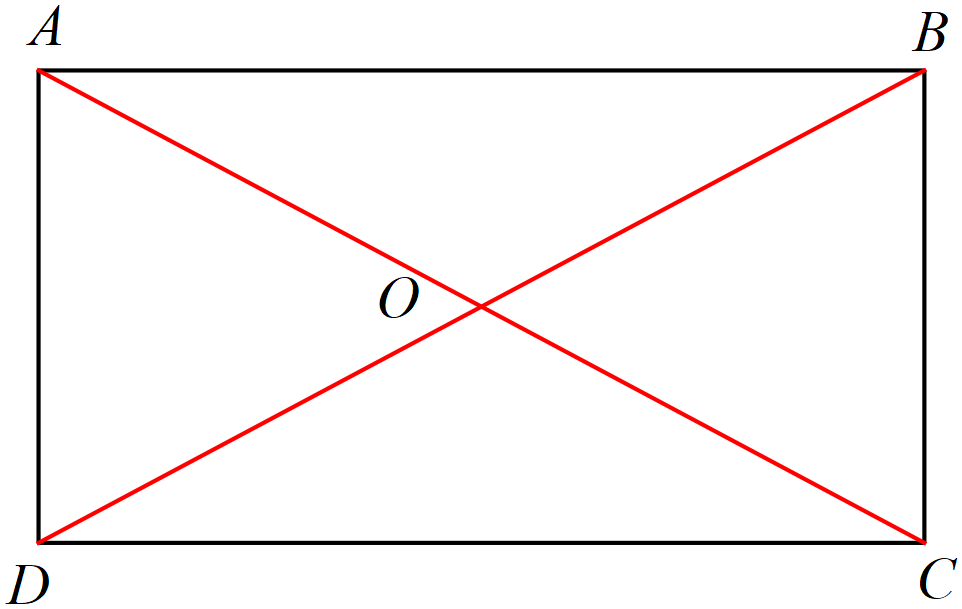
Next, in the rectangle we know that the opposite sides for example AB and CD here will be equal and parallel. Also, it is known that the alternate angles of the parallel sides are equal. So, we can say that the alternate angles \[\angle OBA=\angle ODC\]are equal. Also, we can say that the alternate angles \[\angle OAB=\angle OCD\]as they are lying with the two parallel lines AB and CD.
Now, we have already seen that the line AB=CD as they are the opposite sides of the rectangle and must be equal to make it a rectangle. As shown below:
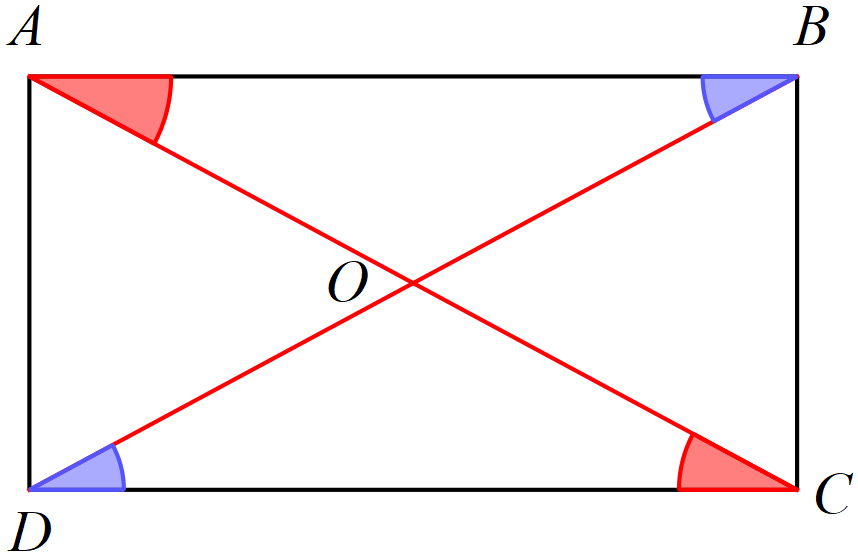
So, now in triangle DOC and triangle BOA, we have:
\[\angle OBA=\angle ODC\]alternate angles.
\[\angle OAB=\angle OCD\] alternate angles.
AB=CD opposite sides of rectangle.
Hence, using the ASA congruence criteria we can say that triangle DOC and triangle BOA are congruent and hence CO = AO and DO =BO (cpct) because corresponding parts of congruent triangles are also equal. So this shows that the diagonals are getting bisected at intersection point O. So finally, the statement which says that the diagonals of a rectangle bisects each other is true.
So, the correct answer is option A.
Note: It can be noted that the diagonals of a rectangle bisect each other but they are not perpendicular to each other. Also, a rectangle should not be confused with the parallelogram.
Complete step-by-step answer:
In the question, we have to check if the statement which says that the diagonals of a rectangle bisects each other is true or not. So here we will first draw the rectangle and the diagonals as shown below:
Next, in the rectangle we know that the opposite sides for example AB and CD here will be equal and parallel. Also, it is known that the alternate angles of the parallel sides are equal. So, we can say that the alternate angles \[\angle OBA=\angle ODC\]are equal. Also, we can say that the alternate angles \[\angle OAB=\angle OCD\]as they are lying with the two parallel lines AB and CD.
Now, we have already seen that the line AB=CD as they are the opposite sides of the rectangle and must be equal to make it a rectangle. As shown below:
So, now in triangle DOC and triangle BOA, we have:
\[\angle OBA=\angle ODC\]alternate angles.
\[\angle OAB=\angle OCD\] alternate angles.
AB=CD opposite sides of rectangle.
Hence, using the ASA congruence criteria we can say that triangle DOC and triangle BOA are congruent and hence CO = AO and DO =BO (cpct) because corresponding parts of congruent triangles are also equal. So this shows that the diagonals are getting bisected at intersection point O. So finally, the statement which says that the diagonals of a rectangle bisects each other is true.
So, the correct answer is option A.
Note: It can be noted that the diagonals of a rectangle bisect each other but they are not perpendicular to each other. Also, a rectangle should not be confused with the parallelogram.