Question

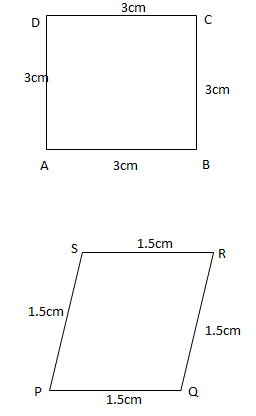
State whether the quadrilaterals are similar or not

Answer 1

Hint: Two polygons having same number of sides can be said to be similar if
The corresponding sides of the two polygon are equal or
The corresponding angles of the two polygons are equal.

Complete step-by-step answer:
It is given that the two diagrams on the sides of the two quadrilaterals are not equal because each side of quadrilateral $PQRS$ is $1.5cm$ and each side of the quadrilateral $ABCD$ is $3cm$.
So the first condition is not fulfilled.
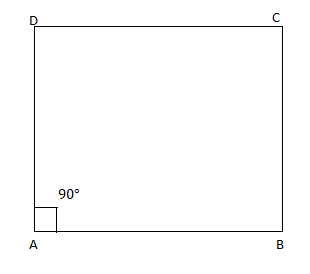
In the quadrilateral $ABCD$ we see that
$\angle DAB = 90_{}^o$

In the quadrilateral $PQRS$ we see that-
$\angle SPQ \ne 90_{}^o$
Therefore, the second condition is also not fulfilled
Thus, it is confirmed that both the quadrilaterals are not similar.

Note: There are six types of quadrilateral like square, rhombus, parallelogram, trapezium, rectangle and cyclic quadrilateral and all of them have four sides but different properties.
It must be kept in mind always that two polygons will be treated as similar only if the corresponding sides of both the polygons are equal or the corresponding angles of both the polygons are equal.
In case of squares all the sides and angles are equal and the diagonals are in the right angle to each other. In the case of rhombus all the sides are equal but the adjacent angles are supplementary.
Trapezium also has four sides but is not equal in length and its base is parallel to each other.
In case of parallelogram opposite sides are equal and parallel to each other.
In case of rectangles opposite sides are equal and parallel and all the angles of a rectangle are right angles.