
Statement 1: Eccentricity of an ellipse whose length of latus rectum is the same as the distance between its foci, is $2\sin {18^ \circ }$
Statement 2: For \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\], eccentricity \[e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} \]
A). Statement 1 is true, Statement 2 is true and Statement 2 is the correct explanation for statement 1.
B). Statement 1 is true, Statement 2 is true and Statement 2 is not the correct explanation for statement 1.
C). Statement 1 is true, Statement 2 is false.
D). Statement 1 is false, Statement 2 is true.
E). Both statements are false.
Answer
472.5k+ views
Hint: Start by making an ellipse with all the important details marked. Find a relation between foci and latus rectum and use the formula of eccentricity to find out the desired value. Check the validity of each statement and mark the correct option.
Complete step-by-step answer:
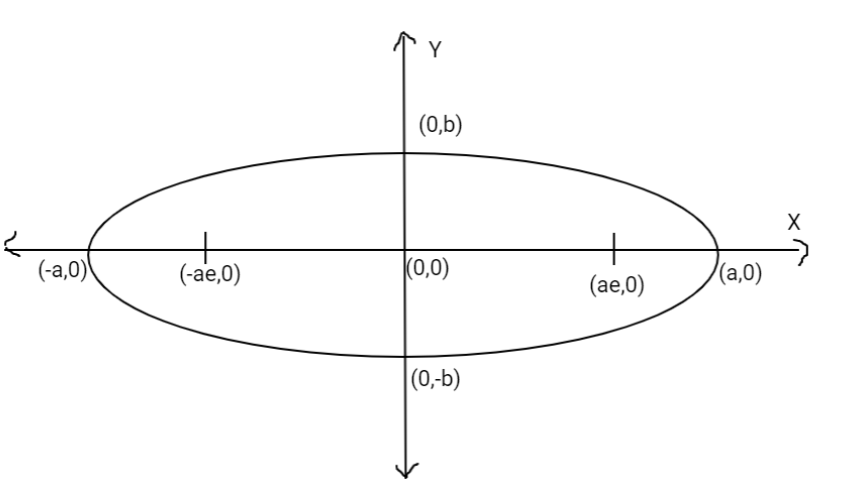
In order to answer or verify any statement, we need to understand about Ellipse first, Discuss its Focii, Eccentricity, major and minor axes.
Refer diagram for better understanding.
$[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1;{\text{ where }}a > b \to eqn(1)]$
a > b means the major axis lies on x-axis.
Focus (ae,0) and (-ae,0), which gives the distance between foci as 2ae.
Length of latus rectum = $[\dfrac{{2{b^2}}}{a}]$
Eccentricity = $[e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} \to eqn(2)]$
Now, We know that the distance between the foci is equal to the length of the latus rectum.
$[2ae = \dfrac{{2{b^2}}}{a} ]$
$[ \Rightarrow e = \dfrac{{{b^2}}}{{{a^2}}} \to eqn(3)]$
Now, from eqn(2) and eqn(3) , we get
$[\dfrac{{{b^2}}}{{{a^2}}} = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} ]$
Squaring both the sides, we get
$ {\left[ {\dfrac{{{b^2}}}{{{a^2}}}} \right]^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}} \\
\Rightarrow {e^2} = 1 - e \\
\Rightarrow {e^2} + e - 1 = 0 \\ $
Solving this quadratic equation by Discriminant rule[ for any quadratic equation $a{x^2} + bx + c = 0{\text{ , D = }}{b^2} - 4ac$and roots of the equation when D>0 is $ = \dfrac{{ - b \pm \sqrt D }}{{2a}}]$
We’ll obtain two values of e
$[e = \dfrac{{ - 1 \pm \sqrt 5 }}{2}]$
But the eccentricity can never be negative
$[\therefore e = \dfrac{{ - 1 + \sqrt 5 }}{2}]$
This can also be written as
$[e = 2 \times (\dfrac{{ - 1 + \sqrt 5 }}{4})]$
And we know that $[\sin {18^ \circ } = \dfrac{{ - 1 + \sqrt 5 }}{4}]$
Which shows $[e = 2\sin {18^ \circ }. ]$
This is in accordance with statement 1.
Therefore, Both the statements are true and statement 2 is the correct explanation of statement 1.
So, option A is the correct answer.
Note: All the properties and features of Parabola, Ellipse, Circle, Hyperbola must be known very well in order to solve such similar problems. Attention is to be given while forming the relations and must consider the possibilities of negative or positive quantities. For e.g. Eccentricity cannot be negative, Always take positive value.
Complete step-by-step answer:
In order to answer or verify any statement, we need to understand about Ellipse first, Discuss its Focii, Eccentricity, major and minor axes.
Refer diagram for better understanding.
$[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1;{\text{ where }}a > b \to eqn(1)]$
a > b means the major axis lies on x-axis.
Focus (ae,0) and (-ae,0), which gives the distance between foci as 2ae.
Length of latus rectum = $[\dfrac{{2{b^2}}}{a}]$
Eccentricity = $[e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} \to eqn(2)]$
Now, We know that the distance between the foci is equal to the length of the latus rectum.

$[2ae = \dfrac{{2{b^2}}}{a} ]$
$[ \Rightarrow e = \dfrac{{{b^2}}}{{{a^2}}} \to eqn(3)]$
Now, from eqn(2) and eqn(3) , we get
$[\dfrac{{{b^2}}}{{{a^2}}} = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} ]$
Squaring both the sides, we get
$ {\left[ {\dfrac{{{b^2}}}{{{a^2}}}} \right]^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}} \\
\Rightarrow {e^2} = 1 - e \\
\Rightarrow {e^2} + e - 1 = 0 \\ $
Solving this quadratic equation by Discriminant rule[ for any quadratic equation $a{x^2} + bx + c = 0{\text{ , D = }}{b^2} - 4ac$and roots of the equation when D>0 is $ = \dfrac{{ - b \pm \sqrt D }}{{2a}}]$
We’ll obtain two values of e
$[e = \dfrac{{ - 1 \pm \sqrt 5 }}{2}]$
But the eccentricity can never be negative
$[\therefore e = \dfrac{{ - 1 + \sqrt 5 }}{2}]$
This can also be written as
$[e = 2 \times (\dfrac{{ - 1 + \sqrt 5 }}{4})]$
And we know that $[\sin {18^ \circ } = \dfrac{{ - 1 + \sqrt 5 }}{4}]$
Which shows $[e = 2\sin {18^ \circ }. ]$
This is in accordance with statement 1.
Therefore, Both the statements are true and statement 2 is the correct explanation of statement 1.
So, option A is the correct answer.
Note: All the properties and features of Parabola, Ellipse, Circle, Hyperbola must be known very well in order to solve such similar problems. Attention is to be given while forming the relations and must consider the possibilities of negative or positive quantities. For e.g. Eccentricity cannot be negative, Always take positive value.
Recently Updated Pages
Can anyone list 10 advantages and disadvantages of friction

What are the Components of Financial System?

How do you arrange NH4 + BF3 H2O C2H2 in increasing class 11 chemistry CBSE

Is H mCT and q mCT the same thing If so which is more class 11 chemistry CBSE

What are the possible quantum number for the last outermost class 11 chemistry CBSE

Is C2 paramagnetic or diamagnetic class 11 chemistry CBSE

Trending doubts
Which is not a source of freshwater 1 Glaciers and class 11 chemistry CBSE

10 examples of friction in our daily life

The correct order of melting point of 14th group elements class 11 chemistry CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the specific heat capacity of ice water and class 11 physics CBSE




