
Statement 1: The graph between velocity and displacement for a harmonic oscillator is an ellipse.
Statement 2: Velocity does not change uniformly with displacement in harmonic motion.
A) Statement 1 is false, statement 2 is true
B) Statement 1 is true, statement 2 is true, Statement 2 is the correct explanation for statement 1
C) Statement 1 is true, statement 2 is true, Statement 2 is not the correct explanation for statement 1
D) Statement 1 is false, statement 2 is false.
Answer
467.4k+ views
Hint: Velocity of a particle in a simple harmonic motion can be given in terms of amplitude, angular velocity and position of the particle. Squaring and dividing the equation accordingly, we can convert the equation into the equation for ellipse.
Formula used:
Complete step-by-step solution:
In a simple harmonic motion, velocity is given by,
Where,
Then,
Dividing both sides of the equation 1 by
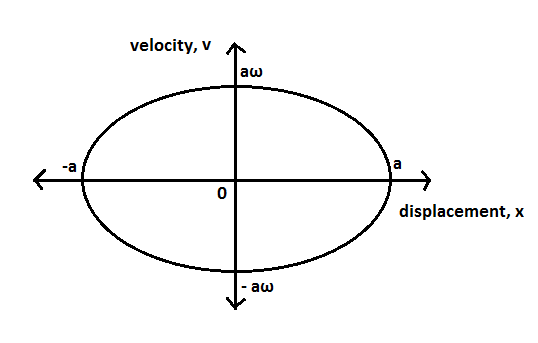
Velocity-displacement graph of a harmonic oscillator.
We have equation for ellipse as,
Comparing equations 2 and 3, we can say that the graph between velocity and displacement for a harmonic oscillator is an ellipse.
From the elliptical graph we can understand that the velocity is not changing uniformly with displacement in harmonic motion.
Hence, statement 1 is true, statement 2 is true, Statement 2 is not the correct explanation for statement 1.
Hence the answer is option C.
Note: The position of a particle in a simple harmonic motion is given by,
Where,
Then,
Squaring the equation on both sides,
Velocity in a simple harmonic motion is given by,
Then,
Squaring the equation on both sides,
We have,
Then,
Equation for ellipse is given by,
Comparing the equations 1 and 2 we can see that the graph between velocity and displacement for a harmonic oscillator is an ellipse.
Formula used:
Complete step-by-step solution:
In a simple harmonic motion, velocity is given by,
Where,
Then,
Dividing both sides of the equation 1 by

Velocity-displacement graph of a harmonic oscillator.
We have equation for ellipse as,
Comparing equations 2 and 3, we can say that the graph between velocity and displacement for a harmonic oscillator is an ellipse.
From the elliptical graph we can understand that the velocity is not changing uniformly with displacement in harmonic motion.
Hence, statement 1 is true, statement 2 is true, Statement 2 is not the correct explanation for statement 1.
Hence the answer is option C.
Note: The position of a particle in a simple harmonic motion is given by,
Where,
Then,
Squaring the equation on both sides,
Velocity in a simple harmonic motion is given by,
Then,
Squaring the equation on both sides,
We have,
Then,
Equation for ellipse is given by,
Comparing the equations 1 and 2 we can see that the graph between velocity and displacement for a harmonic oscillator is an ellipse.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




