Question

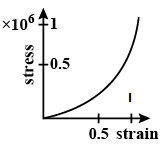
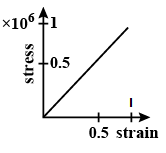
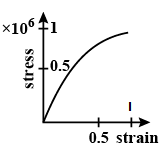
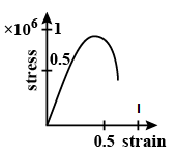
Stress VS Strain for the elastic stress tissue of aorta, the large tube (vessel) carrying blood from the heart, will be: (stress is proportional to the square of the strain for the elastic tissue of the aorta)
$A.$

$B.$

$C.$

$D.$

Answer 1

Hint: We know that the stress is defined as the restoring force per unit area. The strain is the measure of deformation produced under the action of a load. It is given in the problem that the stress is proportional to the square of the strain for the elastic tissue of the aorta tissue.

Complete step-by-step solution:
We know that the restoring force per unit area is called stress.
Mathematically, it can be written as $\sigma =\dfrac{F}{A}$ . Where, $\sigma $ is the stress, $F$ is Force and $A$ is area of cross section.
The ratio of deformation produced to the original dimensions is called strain.
Mathematically, it can be written as $\varepsilon =\dfrac{dl}{l}$ . Where, $\varepsilon $ is strain produced, $dl$ represents change in length and $l$ is original length.
We know that aorta tissue is an elastic artery .It is given in the problem that the stress is directly proportional to the square of the strain for the elastic tissue of the aorta. From the basic knowledge of graphs we know that the graph of a square function is of quadratic type and that of linear function is a straight line. We can conclude that the graph will be of quadratic equation type. From the options given above we can easily identify that only option $(A)$ is correct which is represented with the following stress VS strain diagram

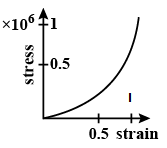
Additional Information:
We should know the difference between an elastic body and a plastic body.
The property of the body by virtue of which it regains its original shape and size after removing the deforming load is called elasticity. If the body regains its original shape and size completely, after the removal of the deforming load, then the body is said to be perfectly elastic.
The property of the body by virtue of which it does not retain its original shape and size after removing the deforming load is called plasticity. If the body does not have any tendency to recover its original shape and size, it is called perfectly plastic.

Note: In solving these types of problems of graphs we should apply the basics of graphs. Graphs of linear equations will be used for linear relationship, quadratic equations for the relationships in terms of square and so on.