Question

Suppose a player hits several baseballs. Which baseball will be in the air for the longest time?
A. The one with the farthest range.
B. The one which reaches maximum height.
C. The one with the greatest initial velocity.
D. The one leaving the bat at 45 degree with respect to the ground.

Answer 1

Hint-This is the case of projectile motion. By analyzing the equations for time of flight, range and the height of the projectile, we can find the situation for which the time of flight will be maximum.

Complete step by step solution:
It is given that a player hits several baseballs. We need to find the baseball which will have the longest time in air.

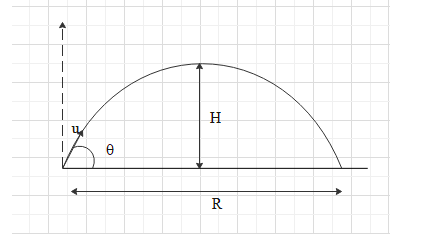
This is a case of projectile motion. We know that the time taken for the flight in the projectile motion is given as

$T = \dfrac{{2u\sin \theta }}{g}$

Where u is initial velocity, $\theta $ is the angle with which it is projected and g is acceleration due to gravity.
The height of the projectile is given as

$H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$

And the range of the projectile is given as

$R = \dfrac{{{u^2}\sin 2\theta }}{g}$

Now let us analyze the options one by one.

(a)In the first option it is given that the one with the farthest range will have the maximum time.

For the range to be maximum $\sin 2\theta $ should be maximum.

$ \Rightarrow \sin 2\theta = 1$

We know that the value of sin is maximum for 90 degrees.

$ \Rightarrow 2\theta = {90^ \circ }$
$ \Rightarrow \theta = {45^ \circ }$

Hence, we get the angle of projection as ${45^ \circ }$ .

But for the time to be maximum we need angle to be ${90^ \circ }$

Since, $\sin \theta $ appears in the equation for time. So, if the angle of projection is ${45^ \circ }$ we will not get maximum value for time.

Hence the first option is wrong.

(b)In the second option it is given that the one which reaches a maximum height will have the maximum time.

From the equation for height we can see that for height to be the maximum value of $\theta $ should be ${90^ \circ }$. Since $\sin {90^ \circ } = 1$ .

This value of $\theta $ gives the maximum value for time also. Hence this option is correct.

(c)The option C states that the baseball with greatest initial velocity will have maximum time is not correct because even if the velocity is high if the value of $\sin \theta $ is small then the time taken will not be maximum.

(d)Option D states the one leaving at ${45^ \circ }$ with respect to ground is also wrong because we need $\theta = {90^ \circ }$ for maximum time.

So, the correct answer is option B.

Note: Remember that the maximum value of a sine function is one.
The angle for which we get this maximum value for sine function is ${90^ \circ }$. Hence if a projectile is projected at ${90^ \circ }$ it will take the longest time to come back. The height will also be maximum if we project it at ${90^ \circ }$. It will cover the maximum range when it is projected at ${45^ \circ }$.