Question

Suppose in an exceedingly circular motion of a particle , the tangential acceleration of the particle is given by \[at\Rightarrow 9m/{{s}^{2}}\]. The radius of the circle is 4m. The particle was initially at rest . Find the time after which acceleration of the particle makes an angle of \[{{45}^{\circ }}\] with the radial accelerations is –
A. \[\dfrac{1}{3}s\]
B. \[\dfrac{2}{3}s\]
C. \[\dfrac{4}{3}s\]
D. \[1s\]

Answer 1

Hint: We know that the radial acceleration is equal to the rate of change in velocity . The change which generates in speed during the non uniform circular motion known as tangential acceleration.

Complete step-by-step solution:
let's draw a diagram of this question to solve this question-

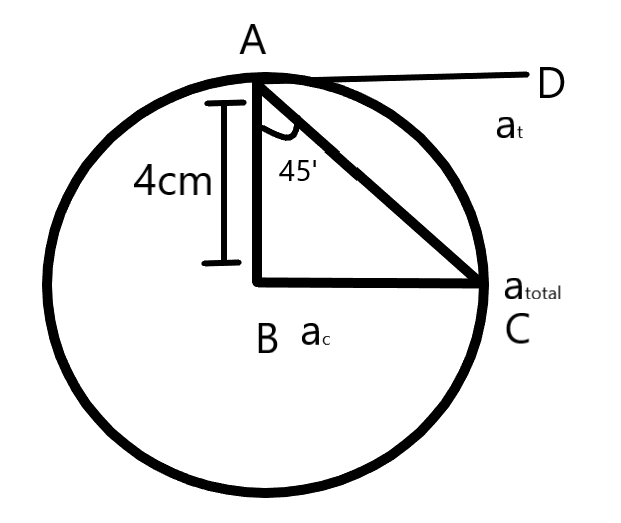
here in this problem , tangential acceleration = \[9m/{{s}^{2}}\]
Radius =\[4m\]
from the fig we get triangle ABC ,
\[\begin{align}
  & \tan {{45}^{\circ }}\Rightarrow \dfrac{at}{ac} \\
 & or,1\Rightarrow \dfrac{9}{ac} \\
 & or,ac\Rightarrow 9m/{{s}^{2}} \\
\end{align}\]
Now , we know that tangential acceleration is
\[at\Rightarrow \dfrac{dv}{dt}\]
\[or,dv\Rightarrow at.dt\]
\[or,\int_{0}^{v}{dv\Rightarrow \int\limits_{0}^{t}{9dt}}\]
\[or,v\Rightarrow 9t\] \[m/s\]
Again , we know that centripetal acceleration \[\left( ac \right)=\dfrac{{{v}^{2}}}{r}\]
 Now , using \[(ac)=(at)\] we get

\[\dfrac{{{v}^{2}}}{r}\Rightarrow \dfrac{dv}{dt}\]
\[or,\dfrac{{{(9t)}^{2}}}{4}\Rightarrow 9\]
\[or,\dfrac{81t}{4}\Rightarrow 9\]
\[or,{{1}^{2}}\Rightarrow \dfrac{4}{9}\]
\[or,t\Rightarrow \dfrac{2}{3}\sec \]
Therefore, the correct option is B) \[\dfrac{2}{3}s\].

Note: During circular motion the speed vector changes its direction at each point on the circle . This suggests that the tangential component of acceleration is always non-zero.