
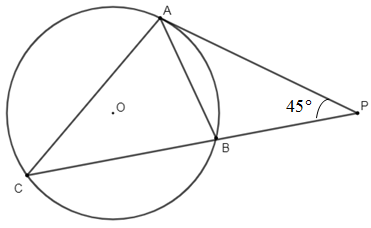
Tangent segment $\overline{PA}$ and secant segment $\overline{PBC}$ are drawn to circle$O$, and $\overline{AB}$ and $\overline{AC}$ are chords. If $m\angle P=45{}^\circ $ and $m\overset\frown{AC}:m\overset\frown{AB}=5:2$, find –
(a) $m\angle PAC$ (b) $m\angle ACB$

Answer
585.3k+ views
Hint: This question is based on geometry only. Here we assume angles $\angle AOC$ and $\angle COB$ according to the ratio of arc $\overset\frown{AC}$ and $\overset\frown{AB}$ given in the question. Then using following properties, we calculate all angles:-
(i) Ratio between two arcs and ratio between angles subtended by corresponding arcs at centre are equal.
$\dfrac{m\overset\frown{AB}}{m\overset\frown{AC}}=\dfrac{m\angle AOB}{m\angle AOC}$
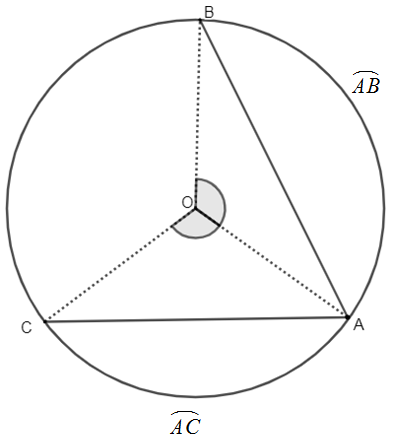
(ii) Angle between tangent and line joining centre and point of contact or tangency is right angle or $90{}^\circ $.
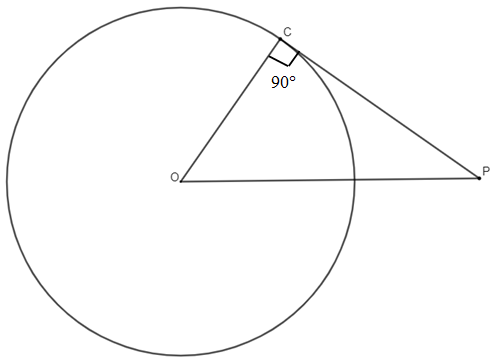
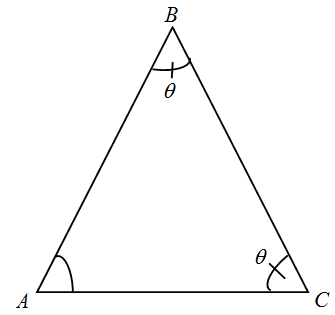
(iii) In any triangle, angles in front of any two equal sides are equal.
$AB=AC$
$\Rightarrow \angle ABC=\angle ACB$
Complete step-by-step answer:
Now, according to the question, $\angle APB=45{}^\circ $ and the ratio between arc $\overset\frown{AC}$ and $\overset\frown{AB}$ is equal to $5:2$.
We know that ratio between length of arcs and ratio between angles subtended by corresponding arcs at centre are equal.
$\dfrac{m\overset\frown{AC}}{m\overset\frown{AB}}=\dfrac{m\angle AOC}{m\angle AOB}$
$\therefore \dfrac{m\overset\frown{AC}}{m\overset\frown{AB}}=\dfrac{m\angle AOC}{m\angle AOB}=\dfrac{5}{2}$
Let us now assume $\angle AOC$ is $5\theta $ and $\angle AOB$ is $2\theta $.
$\therefore ~\angle AOC=5\theta $ and $\angle AOB=2\theta $
Now, we know that, angle between tangent and radius is always $90{}^\circ $. In the figure below, $PA$ is a tangent on the circle and $AO$ is the radius. Hence, $\angle PAO$ is a right angle.
$\therefore \angle PAO=90{}^\circ $
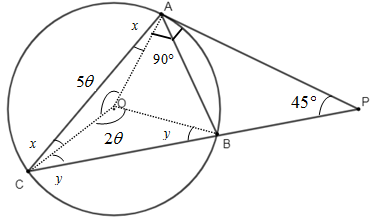
Also, in any triangle angles in front of any two equal sides are equal. So, in$\Delta AOC$, $AO$ and $OC$ are radius. Then,$\angle OAC=\angle OCA$.
And, in$\Delta BOC$, $BO$ and $OC$ are the radius of the circle. So, $BO=OC$. Then, $\angle OBC=\angle OCB$.
Let us assume $\angle OAC=\angle OCA=x{}^\circ $ and $\angle OBC=\angle OCB=y{}^\circ $.
Since the sum of internal angles in any triangle is $180{}^\circ $,in $\Delta AOC$-
$\angle AOC+\angle OAC+\angle OCA=180{}^\circ $
$\Rightarrow 5\theta +x+x=180{}^\circ $
$\Rightarrow 2x=180{}^\circ -5\theta $
\[\Rightarrow x=90{}^\circ -\dfrac{5\theta }{2}\]
And, in $\Delta COB$,
$\angle COB+\angle OBC+\angle OCB=180{}^\circ $
$\Rightarrow 2\theta +y+y=180{}^\circ $
$\Rightarrow 2y=180{}^\circ -2\theta $
$\Rightarrow y=90{}^\circ -\theta $
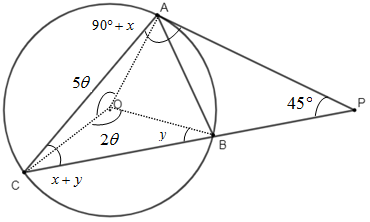
Now, according to figure –
$\angle PAC=90{}^\circ +x$
$\angle ACP=x+y$
$\angle APC=45{}^\circ $
In $\Delta PAC$,
\[\angle PAC+\angle ACP+\angle APC=180{}^\circ \]
$\Rightarrow \left( 90{}^\circ +x \right)+\left( x+y \right)+45{}^\circ =180{}^\circ $
$\Rightarrow 2x+y=45{}^\circ $
$\because x=90{}^\circ -\dfrac{5\theta }{2}$ and $y=90{}^\circ -\theta $
$\Rightarrow 2\left( 90{}^\circ -\dfrac{5\theta }{2} \right)+\left( 90{}^\circ -\theta \right)=45{}^\circ $
$\Rightarrow 180{}^\circ -5\theta +90{}^\circ -\theta =45{}^\circ $
$\Rightarrow 225{}^\circ =6\theta $
$\Rightarrow \theta =\dfrac{225{}^\circ }{6}$
$\Rightarrow \theta =37.5{}^\circ $
So,
$x=90{}^\circ -\dfrac{5\theta }{2}$
$=90{}^\circ -\dfrac{5\times 37.5}{2}$
$=90{}^\circ -\dfrac{187.5{}^\circ }{2}$
$=-3.75{}^\circ $
And,
$y=90{}^\circ -\theta $
$=90{}^\circ -37.5{}^\circ $
$=52.5{}^\circ $
Also, $\angle AOC=5\theta =5\times 37.5=187.5{}^\circ $
$\angle COB=2\theta =2\times 37.5=75{}^\circ $
So, the actual figure will be –
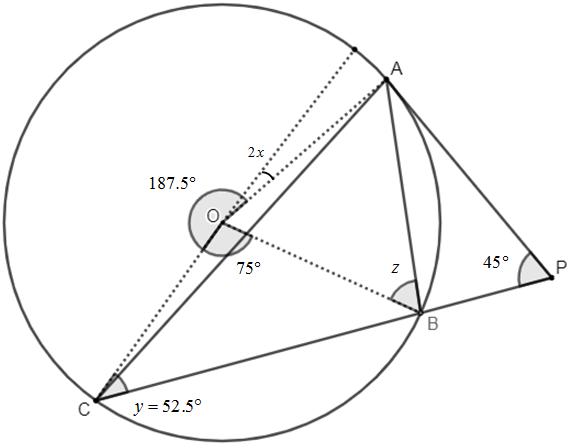
We know that the whole circle subtends an angle of $360{}^\circ $ at the centre.
$\therefore \angle COB+\angle BOA+\angle AOC=360{}^\circ $
$\Rightarrow 75{}^\circ +\angle BOA+187.5{}^\circ =360{}^\circ $
$\Rightarrow \angle BOA=97.5{}^\circ $
Now, $AO$ and $OB$ are the radius of the circle.
$\therefore AO=OB$
We know that in a triangle, angles in front of any two equal sides are equal.
$\Rightarrow \angle OAB=\angle OBA$
Let $\angle OAB=\angle OBA=x{}^\circ $
So, in $\Delta AOB$,
$\angle AOB+\angle OAB+\angle OBA=180{}^\circ $
$\Rightarrow 97.5{}^\circ +z+z=180{}^\circ $
$\Rightarrow 2z=82.5{}^\circ $
$\Rightarrow z=41.25{}^\circ $
$\therefore \angle OAB=\angle OBA=41.25{}^\circ $
Now according to the figure, as $\overline{CBP}$ is a straight line, so
$\angle CBO+\angle OBA+\angle ABP=180{}^\circ $
$\Rightarrow y+z+\angle ABP=180{}^\circ $
$\Rightarrow 52.5{}^\circ +41.25{}^\circ +\angle ABP=180{}^\circ $
$\Rightarrow \angle ABP=86.25{}^\circ $
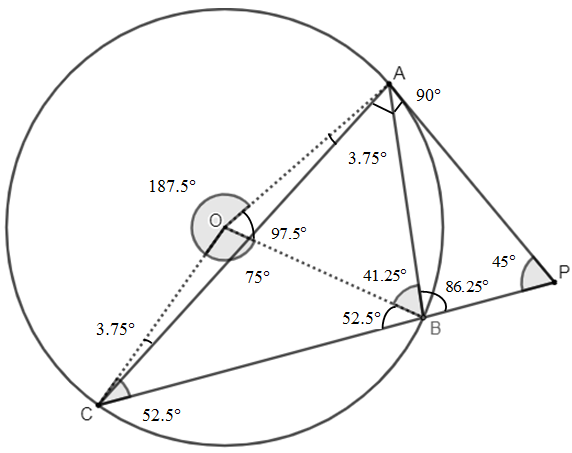
According to the above figure –
$\angle COA=187.5{}^\circ $ (major arc)
$\angle COB=75{}^\circ $ (minor arc)
$\angle BOA=97.5{}^\circ $ (minor arc)
$\angle OCA=3.75{}^\circ =\angle OAC$
$\angle OCB=\angle OBC=52.5{}^\circ $
$\angle OBA=\angle OAB=41.25{}^\circ $
$\angle ABP=86.25{}^\circ $
According to the figure,
$\angle PAC=\angle PAO-\angle CAO$
$\Rightarrow \angle PAC=90{}^\circ -3.75{}^\circ $
$\Rightarrow \angle PAC=86.25{}^\circ $
And,
$\angle ACB=\angle OCB-\angle OCA$
$\Rightarrow \angle ACB=52.5{}^\circ -3.75{}^\circ $
$\Rightarrow \angle ACB=48.75{}^\circ $
Hence, \[m\angle PAC=86.25{}^\circ \]and $\angle ACB=48.75{}^\circ $ .
Note: Students should take care of calculations and all angles carefully. If we take any angle wrong, there will be mistakes in all angle calculations. Here we have to take care of major arcs and minor arcs also.
(i) Ratio between two arcs and ratio between angles subtended by corresponding arcs at centre are equal.
$\dfrac{m\overset\frown{AB}}{m\overset\frown{AC}}=\dfrac{m\angle AOB}{m\angle AOC}$

(ii) Angle between tangent and line joining centre and point of contact or tangency is right angle or $90{}^\circ $.

(iii) In any triangle, angles in front of any two equal sides are equal.
$AB=AC$
$\Rightarrow \angle ABC=\angle ACB$

Complete step-by-step answer:
Now, according to the question, $\angle APB=45{}^\circ $ and the ratio between arc $\overset\frown{AC}$ and $\overset\frown{AB}$ is equal to $5:2$.
We know that ratio between length of arcs and ratio between angles subtended by corresponding arcs at centre are equal.
$\dfrac{m\overset\frown{AC}}{m\overset\frown{AB}}=\dfrac{m\angle AOC}{m\angle AOB}$
$\therefore \dfrac{m\overset\frown{AC}}{m\overset\frown{AB}}=\dfrac{m\angle AOC}{m\angle AOB}=\dfrac{5}{2}$
Let us now assume $\angle AOC$ is $5\theta $ and $\angle AOB$ is $2\theta $.
$\therefore ~\angle AOC=5\theta $ and $\angle AOB=2\theta $
Now, we know that, angle between tangent and radius is always $90{}^\circ $. In the figure below, $PA$ is a tangent on the circle and $AO$ is the radius. Hence, $\angle PAO$ is a right angle.
$\therefore \angle PAO=90{}^\circ $

Also, in any triangle angles in front of any two equal sides are equal. So, in$\Delta AOC$, $AO$ and $OC$ are radius. Then,$\angle OAC=\angle OCA$.
And, in$\Delta BOC$, $BO$ and $OC$ are the radius of the circle. So, $BO=OC$. Then, $\angle OBC=\angle OCB$.
Let us assume $\angle OAC=\angle OCA=x{}^\circ $ and $\angle OBC=\angle OCB=y{}^\circ $.
Since the sum of internal angles in any triangle is $180{}^\circ $,in $\Delta AOC$-
$\angle AOC+\angle OAC+\angle OCA=180{}^\circ $
$\Rightarrow 5\theta +x+x=180{}^\circ $
$\Rightarrow 2x=180{}^\circ -5\theta $
\[\Rightarrow x=90{}^\circ -\dfrac{5\theta }{2}\]
And, in $\Delta COB$,
$\angle COB+\angle OBC+\angle OCB=180{}^\circ $
$\Rightarrow 2\theta +y+y=180{}^\circ $
$\Rightarrow 2y=180{}^\circ -2\theta $
$\Rightarrow y=90{}^\circ -\theta $

Now, according to figure –
$\angle PAC=90{}^\circ +x$
$\angle ACP=x+y$
$\angle APC=45{}^\circ $
In $\Delta PAC$,
\[\angle PAC+\angle ACP+\angle APC=180{}^\circ \]
$\Rightarrow \left( 90{}^\circ +x \right)+\left( x+y \right)+45{}^\circ =180{}^\circ $
$\Rightarrow 2x+y=45{}^\circ $
$\because x=90{}^\circ -\dfrac{5\theta }{2}$ and $y=90{}^\circ -\theta $
$\Rightarrow 2\left( 90{}^\circ -\dfrac{5\theta }{2} \right)+\left( 90{}^\circ -\theta \right)=45{}^\circ $
$\Rightarrow 180{}^\circ -5\theta +90{}^\circ -\theta =45{}^\circ $
$\Rightarrow 225{}^\circ =6\theta $
$\Rightarrow \theta =\dfrac{225{}^\circ }{6}$
$\Rightarrow \theta =37.5{}^\circ $
So,
$x=90{}^\circ -\dfrac{5\theta }{2}$
$=90{}^\circ -\dfrac{5\times 37.5}{2}$
$=90{}^\circ -\dfrac{187.5{}^\circ }{2}$
$=-3.75{}^\circ $
And,
$y=90{}^\circ -\theta $
$=90{}^\circ -37.5{}^\circ $
$=52.5{}^\circ $
Also, $\angle AOC=5\theta =5\times 37.5=187.5{}^\circ $
$\angle COB=2\theta =2\times 37.5=75{}^\circ $
So, the actual figure will be –

We know that the whole circle subtends an angle of $360{}^\circ $ at the centre.
$\therefore \angle COB+\angle BOA+\angle AOC=360{}^\circ $
$\Rightarrow 75{}^\circ +\angle BOA+187.5{}^\circ =360{}^\circ $
$\Rightarrow \angle BOA=97.5{}^\circ $
Now, $AO$ and $OB$ are the radius of the circle.
$\therefore AO=OB$
We know that in a triangle, angles in front of any two equal sides are equal.
$\Rightarrow \angle OAB=\angle OBA$
Let $\angle OAB=\angle OBA=x{}^\circ $
So, in $\Delta AOB$,
$\angle AOB+\angle OAB+\angle OBA=180{}^\circ $
$\Rightarrow 97.5{}^\circ +z+z=180{}^\circ $
$\Rightarrow 2z=82.5{}^\circ $
$\Rightarrow z=41.25{}^\circ $
$\therefore \angle OAB=\angle OBA=41.25{}^\circ $
Now according to the figure, as $\overline{CBP}$ is a straight line, so
$\angle CBO+\angle OBA+\angle ABP=180{}^\circ $
$\Rightarrow y+z+\angle ABP=180{}^\circ $
$\Rightarrow 52.5{}^\circ +41.25{}^\circ +\angle ABP=180{}^\circ $
$\Rightarrow \angle ABP=86.25{}^\circ $

According to the above figure –
$\angle COA=187.5{}^\circ $ (major arc)
$\angle COB=75{}^\circ $ (minor arc)
$\angle BOA=97.5{}^\circ $ (minor arc)
$\angle OCA=3.75{}^\circ =\angle OAC$
$\angle OCB=\angle OBC=52.5{}^\circ $
$\angle OBA=\angle OAB=41.25{}^\circ $
$\angle ABP=86.25{}^\circ $
According to the figure,
$\angle PAC=\angle PAO-\angle CAO$
$\Rightarrow \angle PAC=90{}^\circ -3.75{}^\circ $
$\Rightarrow \angle PAC=86.25{}^\circ $
And,
$\angle ACB=\angle OCB-\angle OCA$
$\Rightarrow \angle ACB=52.5{}^\circ -3.75{}^\circ $
$\Rightarrow \angle ACB=48.75{}^\circ $
Hence, \[m\angle PAC=86.25{}^\circ \]and $\angle ACB=48.75{}^\circ $ .
Note: Students should take care of calculations and all angles carefully. If we take any angle wrong, there will be mistakes in all angle calculations. Here we have to take care of major arcs and minor arcs also.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




