Question

Tangents are drawn to the circle ${x^2} + {y^2} = 1$ at the points where it met by the circles, ${x^2} + {y^2} - \left( {\lambda + 6} \right)x + \left( {8 - 2\lambda } \right)y - 3 = 0$, $\lambda $ being the variable. The locus of the point of intersection of these tangents is
$\left( a \right)2x - y - 10 = 0$
$\left( b \right)x + 2y - 10 = 0$
$\left( c \right)x - 2y + 10 = 0$
$\left( d \right)2x + y - 10 = 0$

Answer 1

Hint: In this particular type of question use the concept that the chord joining the point of intersection of the two given circles is common to the both so the equation of tangents drawn from this point is also the same which meet at the same point so use this concept to reach the solution of the question.

Complete step-by-step answer:

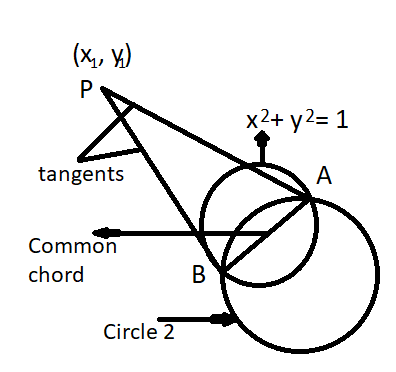
Let the intersection points of two given circles are P and Q, as shown in the figure.
Now let the tangents drawn at these points intersect at point A whose coordinates are (${x_1},{y_1}$).
Now join P and Q as shown in the figure.
So PQ is the common chord between the two circles.
Now as we know that the equation of tangent drawn from an external point (${x_1},{y_1}$) on the circle ${x^2} + {y^2} = 1$ is given as,
$ \Rightarrow x{x_1} + y{y_1} = 1$...................... (1)
Now equation of tangent w.r.t circle ${x^2} + {y^2} - \left( {\lambda + 6} \right)x + \left( {8 - 2\lambda } \right)y - 3 = 0$ from an external point (${x_1},{y_1}$) is given as,
$ \Rightarrow x{x_1} + y{y_1} - \left( {\lambda + 6} \right){x_1} + \left( {8 - 2\lambda } \right){y_1} - 3 = 0$
Now from equation (1) we have,
$ \Rightarrow 1 - \left( {\lambda + 6} \right){x_1} + \left( {8 - 2\lambda } \right){y_1} - 3 = 0$
$ \Rightarrow \left( {\lambda + 6} \right){x_1} - \left( {8 - 2\lambda } \right){y_1} + 2 = 0$...................... (2)
Now as we know that the solution of the parallel lines (i.e. slope is same) or the same line (for example ax + by = c and lx + my = n) is given as $\dfrac{a}{l} = \dfrac{b}{m} = \dfrac{c}{n}$
Now equation (1) and (2) are the same as both are the equations of tangents drawn from the same points P and Q which meet at a point A.
So the solution of these two equation is given as,
$ \Rightarrow \dfrac{x}{{\lambda + 6}} = \dfrac{y}{{ - \left( {8 - 2\lambda } \right)}} = \dfrac{1}{{ - 2}}$....................... (3)
$ \Rightarrow \dfrac{y}{{ - \left( {8 - 2\lambda } \right)}} = \dfrac{1}{{ - 2}}$
Now simplify this equation we have,
$ \Rightarrow 2y = 8 - 2\lambda $
$ \Rightarrow y = 4 - \lambda $
$ \Rightarrow \lambda = 4 - y$
Now from equation (3) we have,
$ \Rightarrow \dfrac{x}{{\lambda + 6}} = \dfrac{{ - 1}}{2}$
Now in this equation substitute the value of ($\lambda $) we have,
$ \Rightarrow \dfrac{x}{{4 - y + 6}} = \dfrac{{ - 1}}{2}$
$ \Rightarrow - 2x = 4 - y + 6$
$ \Rightarrow 2x - y + 10 = 0$
So this is the required locus of the point of intersection of these tangents.
Hence option (a) is the correct answer.

Note – Whenever we face such types of question the key concept we have to remember is that the solution of the parallel lines (i.e. slope is same) or the same line (for example ax + by = c and lx + my = n) is given as $\dfrac{a}{l} = \dfrac{b}{m} = \dfrac{c}{n}$ , then first find the equation of tangents as above then solve these equations using this property as above solved we will get the required locus of the point of intersection of these tangents.