
How can I tell whether a parabola opens upward or downward?
Answer
453.6k+ views
1 likes
Hint: In order to know whether which side parabola is facing, we have to see its highest order term that is the coefficient of the
Complete step by step solution:
A quadratic function is a second degree polynomial function. The general form of a quadratic function is this:
The graph of a quadratic function is called a parabola.
A parabola is roughly shaped like the letter ‘U’ or upside-down ‘U’.
There is an easy way to tell whether the graph of a quadratic function opens upward or downward:
If the leading coefficient is greater than zero, the parabola opens upward, and if the leading coefficient is less than zero, the parabola opens downward.
We can illustrate with the help of following graphs:
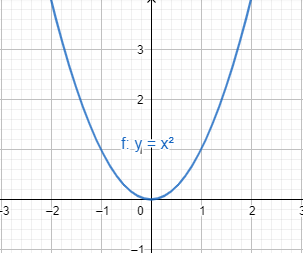
The function above,
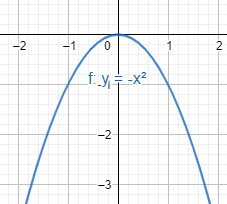
Also, the other function above, has leading coefficient
The standard form of a quadratic function is a little different from the general form.
The standard form of the equation makes it easier to graph.
The standard form of equation is as follows:
In standard form,
The point
The line
A parabola is symmetrical with respect to its axis.
The value of the function at
If
If
That is, if
Note: There will always be a problem while using any quadratic formula, therefore the term that will provide us the overall direction to the equation will be the leading term, or the term with the highest power.
If the term is positive, then as
The result of the equation will become bigger and bigger.
Complete step by step solution:
A quadratic function is a second degree polynomial function. The general form of a quadratic function is this:
The graph of a quadratic function is called a parabola.
A parabola is roughly shaped like the letter ‘U’ or upside-down ‘U’.
There is an easy way to tell whether the graph of a quadratic function opens upward or downward:
If the leading coefficient is greater than zero, the parabola opens upward, and if the leading coefficient is less than zero, the parabola opens downward.
We can illustrate with the help of following graphs:

The function above,

Also, the other function above, has leading coefficient
The standard form of a quadratic function is a little different from the general form.
The standard form of the equation makes it easier to graph.
The standard form of equation is as follows:
In standard form,
The point
The line
A parabola is symmetrical with respect to its axis.
The value of the function at
If
If
That is, if
Note: There will always be a problem while using any quadratic formula, therefore the term that will provide us the overall direction to the equation will be the leading term, or the term with the highest power.
If the term is positive, then as
The result of the equation will become bigger and bigger.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




