Question

The \[{{4}^{th}}\]roots of unity in the argand plane form what shape?

Answer 1

Hint: In this problem, we have to find the shape formed by the \[{{4}^{th}}\]roots of unity in the argand plane. We can first find what are the four roots and the angle between them and we can plot the roots in the argand plane to find the shape formed by the \[{{4}^{th}}\]roots of unity.

Complete step by step answer:
Here we have to find the shape formed by \[{{4}^{th}}\]roots of unity in the argand plane.
We can first find what are the four roots and the angle between them and we can plot the roots in the argand plane to find the shape formed by the \[{{4}^{th}}\]roots of unity.
We know that for \[{{4}^{th}}\]root of unity,
\[\begin{align}
  & \Rightarrow x=\sqrt[4]{1} \\
 & \Rightarrow {{x}^{4}}=1 \\
\end{align}\]
On solving this, we will get
\[\Rightarrow {{x}^{4}}=\cos \dfrac{2\pi }{4}k+i\sin \dfrac{2\pi }{4}k\]
Now we can substitute for the value of k, to find the roots.
Let k = 0, we get
\[\Rightarrow x=\cos \dfrac{2\pi }{4}\left( 0 \right)+i\sin \dfrac{2\pi }{4}\left( 0 \right)=1+0=1\]
Let k = 1, we get
\[\Rightarrow x=\cos \dfrac{2\pi }{4}\left( 1 \right)+i\sin \dfrac{2\pi }{4}\left( 1 \right)=0+i\left( 1 \right)=i\]
Let k = 2, we get
\[\Rightarrow x=\cos \dfrac{2\pi }{4}\left( 2 \right)+i\sin \dfrac{2\pi }{4}\left( 0 \right)=-1+0=-1\]
Let k = -1, we get
\[\Rightarrow x=\cos \dfrac{2\pi }{4}\left( -1 \right)+i\sin \dfrac{2\pi }{4}\left( -1 \right)=0+i\left( -1 \right)=-i\]
Therefore, the fourth roots of unity are \[i,-i,1,-1\].
We can now see that the angle formed here is exactly \[{{90}^{\circ }}\].
We can now plot these roots in the argand plane, we get
 

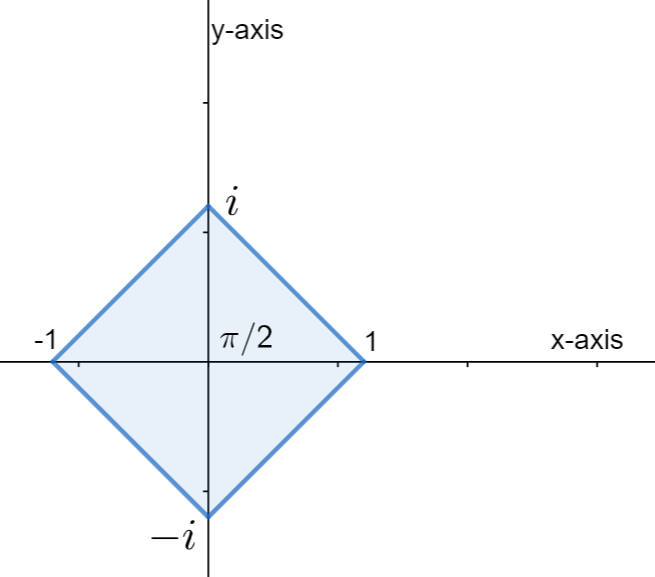
Therefore, the fourth roots of unity form a square.

Note: We should always remember that the fourth roots of unity are \[i,-i,1,-1\] the angle formed here is exactly \[{{90}^{\circ }}\]. Therefore, after plotting, we can see that the fourth roots of unity form a square in the argand plane.