Answer
441.3k+ views
Hint: We need to understand the relation between the acceleration of a body and the displacement of the body. The graph of acceleration versus the time graph can give enough information required for the solution that is needed for this problem.
Complete step-by-step solution
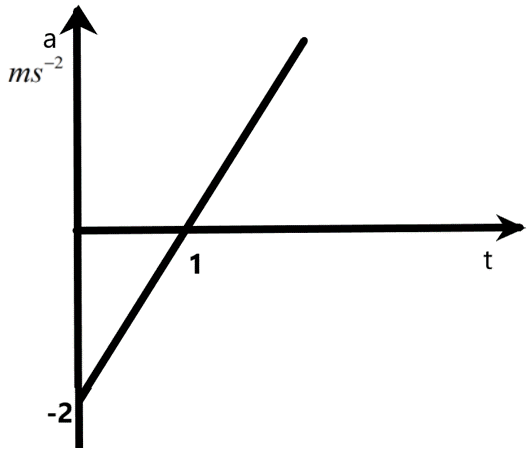
We are given a graph of acceleration of a particle versus the time. We know that the slope of certain graphs given the physical parameters related to the quantities on the graph. In our case, the differential of the graph will not give us any required value.
We know that the area under the graph of an acceleration versus time graph can give the velocity of the particle under consideration. We can derive the required relation in terms of time ‘t’ for the velocity using this idea. The integral of the given graph can give the expression for the velocity. So, we can find the equation of the line as –
\[\begin{align}
& y=mx+c \\
& \Rightarrow y=\dfrac{(0-(-2))}{(1-0)}x+-2 \\
& \text{here,} \\
& y=a,x=t \\
& \therefore a=2t-2 \\
\end{align}\]
We can integrate the above equation to get the velocity on the L.H.S as –
\[\begin{align}
& \int\limits_{{}}^{{}}{a}=\int{(2t-2})dt \\
& \Rightarrow v={{t}^{2}}-2t+c \\
& \text{initially,} \\
& v=0 \\
& \therefore v={{t}^{2}}-2t \\
\end{align}\]
This is the required expression for velocity in terms of time ‘t’.
(b) We can find the displacement from the above expression very easily. The displacement is the integral of the velocity with time. So, the displacement of the particle is given as –
\[\begin{align}
& v={{t}^{2}}-2t \\
& \Rightarrow s=\int{v}=\int\limits_{t=2s}^{t=4s}{({{t}^{2}}-2t)}dt \\
& \Rightarrow s=\left[ \dfrac{{{t}^{3}}}{3} \right]_{2}^{4}-[{{t}^{2}}]_{2}^{4} \\
& \therefore s=6.67m \\
\end{align}\]
The displacement of the particle between the two seconds of motion from 2s to 4s is 6.67m. This is the required solution.
Note: The expression for the acceleration of a particle can give the complete details of the motion of a particle as we have seen in this problem. The same is possible for any of the expressions for the displacement of the particle or the velocity of the particle is given.
Complete step-by-step solution
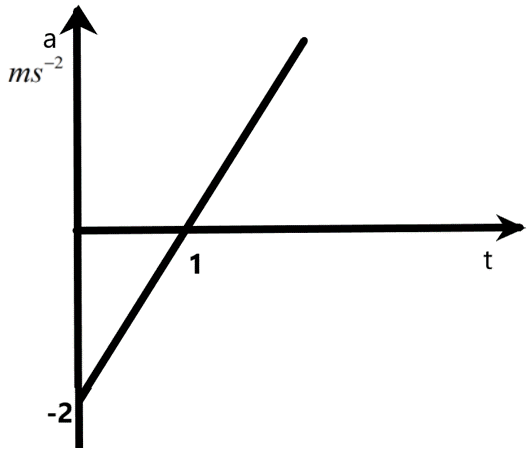
We are given a graph of acceleration of a particle versus the time. We know that the slope of certain graphs given the physical parameters related to the quantities on the graph. In our case, the differential of the graph will not give us any required value.

We know that the area under the graph of an acceleration versus time graph can give the velocity of the particle under consideration. We can derive the required relation in terms of time ‘t’ for the velocity using this idea. The integral of the given graph can give the expression for the velocity. So, we can find the equation of the line as –
\[\begin{align}
& y=mx+c \\
& \Rightarrow y=\dfrac{(0-(-2))}{(1-0)}x+-2 \\
& \text{here,} \\
& y=a,x=t \\
& \therefore a=2t-2 \\
\end{align}\]
We can integrate the above equation to get the velocity on the L.H.S as –
\[\begin{align}
& \int\limits_{{}}^{{}}{a}=\int{(2t-2})dt \\
& \Rightarrow v={{t}^{2}}-2t+c \\
& \text{initially,} \\
& v=0 \\
& \therefore v={{t}^{2}}-2t \\
\end{align}\]
This is the required expression for velocity in terms of time ‘t’.
(b) We can find the displacement from the above expression very easily. The displacement is the integral of the velocity with time. So, the displacement of the particle is given as –
\[\begin{align}
& v={{t}^{2}}-2t \\
& \Rightarrow s=\int{v}=\int\limits_{t=2s}^{t=4s}{({{t}^{2}}-2t)}dt \\
& \Rightarrow s=\left[ \dfrac{{{t}^{3}}}{3} \right]_{2}^{4}-[{{t}^{2}}]_{2}^{4} \\
& \therefore s=6.67m \\
\end{align}\]
The displacement of the particle between the two seconds of motion from 2s to 4s is 6.67m. This is the required solution.
Note: The expression for the acceleration of a particle can give the complete details of the motion of a particle as we have seen in this problem. The same is possible for any of the expressions for the displacement of the particle or the velocity of the particle is given.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

What is the meaning of celestial class 10 social science CBSE

What causes groundwater depletion How can it be re class 10 chemistry CBSE

Under which different types can the following changes class 10 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

In the tincture of iodine which is solute and solv class 11 chemistry CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE