Question

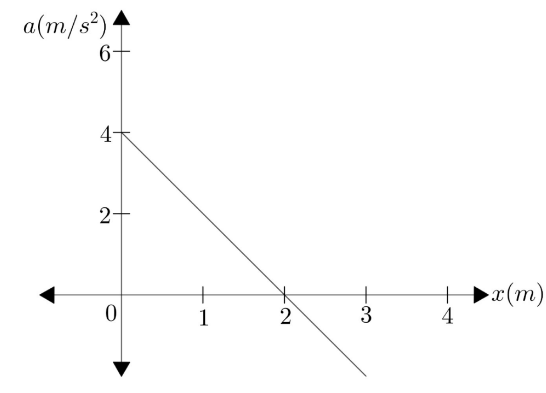
The acceleration-position graph of a particle moving in a straight line along $x-axis$ is shown in figure. The particle starts from rest at origin. The maximum speed of particle is

A. $2m{{s}^{-1}}$
B. $2\sqrt{2}m{{s}^{-1}}$
C. $4m{{s}^{-1}}$
D. $4\sqrt{2}m{{s}^{-1}}$

Answer 1

Hint: From the graph given here, we need to find the equation of the line in terms of acceleration and distance. Using the equation, we can derive the equation for speed. From which the maximum speed can be calculated by taking the first derivative of the equation equal to zero.

Complete step by step answer:
Here, we are given a graph with acceleration on the $y-axis$ and distance on the $x-axis$ . The graph shows a straight line that intersects the acceleration axis $(y-axis)$ at $a=4m{{s}^{-2}}$ and distance axis $(x-axis)$ at $x=2m$
We know that the general equation of a line is $y=mx+c$
where, $y$ = component on the $y-axis$ = Acceleration $(a)$
$x$ = component on the $x-axis$ = Distance $(x)$
$c$ = $y$ - intercept of the line = $4$
$m$ = slope of the line = $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Slope can be found by considering the points $(0,4)$ and $(2,0)$ through which the line passes.
$m=\dfrac{0-4}{2-0}$
$\Rightarrow m=-2$
From these values, we get the equation of the graph given here as
$a=-2x+4$ …… $(1)$

Now, we know that acceleration can be represented in terms of velocity as $a=\dfrac{dv}{dt}$
$\Rightarrow \dfrac{dv}{dt}=-2x+4$
As, the right hand side equation is in terms of distance, we need a factor of distance on left hand side, which can be obtained by multiplying $dx\;$ in the numerator and the denominator
$\Rightarrow \dfrac{dv}{dt}\times \dfrac{dx}{dx}=-2x+4$
$\Rightarrow \dfrac{dv}{dx}\times \dfrac{dx}{dt}=-2x+4$
But we know that $\dfrac{dx}{dt}=v$
$\Rightarrow v\dfrac{dv}{dx}=-2x+4$
Now, multiplying both sides with $dx\;$ ,
$\Rightarrow vdv=\left( -2x+4 \right)dx$

Applying integration on both sides. Here, we are given that the particle starts from rest from the origin. Hence, the limits for speed will be $v=0$ to $v=v$ and the limits for distance will be $x=0$ to $x=x$
$\int\limits_{0}^{v}{vdv}=\int\limits_{0}^{x}{\left( -2x+4 \right)dx}$
$\Rightarrow \left[ \dfrac{{{v}^{2}}}{2} \right]_{0}^{v}=\left[ \dfrac{-2{{x}^{2}}}{2}+4x \right]_{0}^{x}$
Applying the limits,
$\Rightarrow \dfrac{{{v}^{2}}}{2}=-{{x}^{2}}+4x$
$\Rightarrow {{v}^{2}}=-2{{x}^{2}}+8x$
Applying square root on both sides,
$\Rightarrow v=\sqrt{-2{{x}^{2}}+8x}$ …… $(2)$
This is the equation of speed in terms of distance.

Now, here we need to find the maximum speed. We know that for maximum value, the first derivative of the equation will be equal to zero. Hence, now we need to equate the first derivative of the equation of speed to zero. Differentiating the equation $(2)$ with respect to $x$
$\dfrac{dv}{dx}=\dfrac{d}{dx}\left( \sqrt{-2{{x}^{2}}+8x} \right)$
$\Rightarrow \dfrac{dv}{dx}=\dfrac{1}{2\sqrt{-2{{x}^{2}}+8x}}\times -4x+8$
Equating the above equation to zero,
$\Rightarrow \dfrac{-4x+8}{2\sqrt{-2{{x}^{2}}+8x}}=0$
Hence, for the above value to be zero, the numerator will be zero.
$\Rightarrow -4x+8=0$
$\Rightarrow x=2$
Now, to find the maximum speed, we will substitute the above value in the equation $(2)$
${{v}_{\max }}=\sqrt{-2{{(2)}^{2}}+8(2)}$
$\therefore {{v}_{\max }}=2\sqrt{2}m{{s}^{-1}}$

Hence, the correct answer is option B.

Note: Here, while taking the first derivative of the equation of speed, we should remember that the equation is in terms of distance and thus we will take the differentiation in terms of distance. We can verify if the solution of the first derivative will give maximum speed or not by taking the second derivative of the equation of speed. For maximum speed, by substituting the solution, we will get a negative value.