Question

The adjacent sides of a parallelogram are $36{\text{cm}}$ and $27{\text{cm}}$ in length. If the perpendicular distance between the shorter sides is $12{\text{cm}}$, find the distance between the longer sides.

Answer 1

Hint: Here, we will first find the area of the parallelogram with the shorter side as the base and the given perpendicular distance as the height. Then we will find the area using the longer side as the base and the distance between longer sides as the height. We will then equate these areas and solve further to find the required distance between the longer sides.

Formula Used:
Area of parallelogram $A = {\text{base}} \times {\text{height}}$

Complete step-by-step answer:
In a parallelogram, opposite sides are parallel and equal.
It is given that the adjacent sides of a parallelogram are $36{\text{cm}}$ and $27{\text{cm}}$ in length. So,
The longer side, $L = 36{\text{cm}}$
The shorter side, $l = 27{\text{cm}}$
Now, the perpendicular distance between the shorter sides is $12{\text{cm}}$.

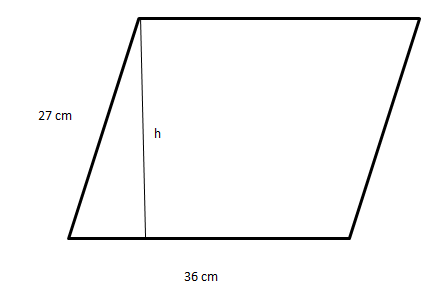
We will now find the area of the parallelogram.
In this case, the base is the shorter side, i.e. $27{\text{cm}}$ and the height is the perpendicular distance between the shorter sides, i.e. $12{\text{cm}}$.
Therefore using the formula of area of parallelogram $A = {\text{base}} \times {\text{height}}$, we get
$A = 27 \times 12$
Now, if we consider the base as the longer side, i.e. $36{\text{cm}}$ and the height to be the perpendicular distance between the longer sides, i.e. $h$.
Therefore using the formula of area of parallelogram $A = {\text{base}} \times {\text{height}}$, we get
$A = 36 \times h$
We know that both the areas are equal because they are the areas of the same parallelogram.
Hence, equating both the areas, we get
$27 \times 12 = 36 \times h$
Dividing both side by 36, we get
\[ \Rightarrow h = \dfrac{{27 \times 12}}{{36}}\]
Simplifying the expression, we get
\[ \Rightarrow h = \dfrac{{27}}{3} = 9{\text{cm}}\]
Therefore, the distance between the longer sides, $h = 9{\text{cm}}$.
Thus, this is the required answer.

Note: A parallelogram is a quadrilateral in which the pair of opposite sides are parallel and equal to each other. Also, each diagonal in a parallelogram divides it into two congruent triangles. The diagonals of the parallelogram bisect each other and divide each other into two equal parts. This means that if the length of the whole diagonal is for example 6 cm then, after intersecting with another diagonal, it gets divided into two equal parts of 3 cm each.