Question

What will be the angle between $\left( A+B \right)$ and $\left( A\times B \right)$? State the reason also.

Answer 1

Hint: First of all find the sum of two vectors and then figure out the position of the resultant vector with respect to the vectors given. Similarly find out the cross product of the vectors and also find out the angle between the vectors and the resultant. Compare both these facts and reach at the answer. This information will help you to solve this question.

Complete answer:
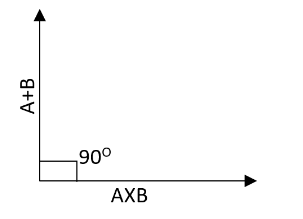
Let us assume that the two vectors we are discussing are given as $A$ and $B$. Let their sum can be written as,
$A+B=sum$
Their sum will be lying in the same plane where the vectors $A$ and $B$ are lying. As they are also found to be non -parallel therefore they can describe a plane and also the cross product between them will be not zero. The cross product of the two vectors can be shown as,
$A\times B=\left| A \right|\left| B \right|\sin \alpha n$
Here $\alpha $ be the angle between $A$ and $B$. The unit vector which is perpendicular to the plane containing $A$ and $B$ is mentioned as $n$. Here the resultant will be perpendicular to the two vectors. Hence we can say that the angle between the $A\times B$ and $A+B$ will be $90{}^\circ $.

Note:
The cross product also known as the vector product is basically the binary operation of two vectors in the three-dimensional space. Cross product can be applicable only in the case of vectors. It has been given two linearly independent vectors $A$and $B$, then their cross product, $A\times B$ will be also a vector which is perpendicular to both the vectors. This will be normal to the plane containing the vectors.