Question

The angle of elevation of an aeroplane from point A on the ground is \[{{60}^{\circ }}\]. After a flight of 15 seconds, the angle of elevation changes to \[{{30}^{\circ }}\]. If the aeroplane is flying at a constant height of \[1500\sqrt{3}\]m, find the speed of the plane in km/hr.

Answer 1

Hint: This question can be solved by considering the similar triangles and then applying the tangent formula to each of the triangles which gives the distance travelled by the flight in 15 seconds as we already know the time now we can calculate the speed of the plane.

Complete step-by-step answer:

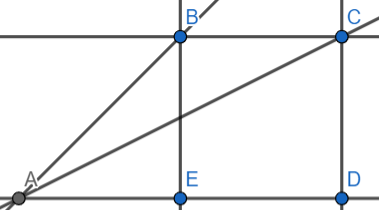
Now from the question we have BE=CD=\[1500\sqrt{3}\] and
\[\begin{align}
  & \angle BAE={{60}^{\circ }} \\
 & \angle CAD={{30}^{\circ }} \\
\end{align}\]
Now, let us assume that AE=x and ED=d
From, trigonometry we already know that in a right angle triangle:

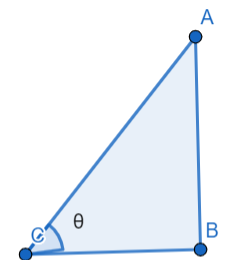
\[\tan \theta =\dfrac{\text{Opposite}}{\text{adjacent}}\]
  Now, from the \[\vartriangle ABE\] we have
\[\tan \theta =\dfrac{BE}{AE}\]
Here, \[\theta ={{60}^{\circ }}\text{, BE=}1500\sqrt{3},\text{ AE=}x\]
Now, by substituting the above values in the tangent formula we get,
\[\begin{align}
  & \Rightarrow \tan {{60}^{\circ }}=\dfrac{1500\sqrt{3}}{x} \\
 & \Rightarrow \sqrt{3}=\dfrac{1500\sqrt{3}}{x}\text{ }\left[ \because \tan {{60}^{\circ }}=\sqrt{3} \right] \\
 & \Rightarrow x=\dfrac{1500\sqrt{3}}{\sqrt{3}} \\
 & \therefore x=1500m \\
\end{align}\]
Now, from the \[\vartriangle ACD\] we have
\[\tan \theta =\dfrac{CD}{AD}\]
Here, we have \[\theta ={{30}^{\circ }}\text{, BE=}1500\sqrt{3},\text{ AE=}x+d\]
Now, by substituting these values in the tangent formula we get,
\[\begin{align}
  & \Rightarrow \tan {{30}^{\circ }}=\dfrac{1500\sqrt{3}}{x+d} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{1500\sqrt{3}}{x}\text{ }\left[ \because \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \right] \\
 & \Rightarrow x+d=1500\sqrt{3}\times \sqrt{3} \\
 & \Rightarrow x+d=1500\times 3 \\
 & \Rightarrow x+d=4500 \\
 & \Rightarrow d=4500-1500\text{ }\left[ \because x=1500 \right] \\
 & \therefore d=3000m \\
\end{align}\]
As we already know the relation between velocity distance and time the formula can be written as:
\[\text{velocity}=\dfrac{\text{distance}}{\text{time}}...............\left( 1 \right)\]
Here, as we know that the distance travelled by the plane in 15 seconds is the distance between the points B and C from the diagram.
As distance between B and C is equal to ED
We know that \[ED=d=3000\]and time = 15s
Now, by substituting these values in the above velocity formula (1) we get,
Let us assume that the speed of plane be v.
\[\begin{align}
  & \Rightarrow v=\dfrac{d}{t} \\
 & \Rightarrow v=\dfrac{3000}{15} \\
 & \therefore v=200m/s \\
\end{align}\]
To convert v in m/s to km/hr we need to apply the following conversion:
\[\begin{align}
  & km/hr\times \dfrac{5}{18}=m/s \\
 & km/hr=\dfrac{18}{5}\times m/s \\
\end{align}\]
Now, by multiplying the value of v with \[\dfrac{18}{5}\]we get the value in terms of km/hr.
\[\begin{align}
  & \Rightarrow v=\dfrac{18}{5}\times 200 \\
 & \Rightarrow v=18\times 40 \\
 & \therefore v=720km/hr \\
\end{align}\]
Hence, the speed of the plane is 720 km/hr.

Note: Considering the angle of elevation and then drawing the figure accordingly is the important step in this problem if we consider the angle of elevations in the other direction like depression or the plane traveling in the reverse direction the result will be wrong because we know that \[{{60}^{\circ }}\]> \[{{30}^{\circ }}\]we need to draw the diagram according to that.
Instead of considering \[x+d\]we can also consider it whole as some other variable and then calculate the complete value then get the distance travelled by the plane in 15 s by subtracting x from the whole distance which also gives the same result.