Question

The angle of elevation of the top of a tower standing on a horizontal plane from point A is \[\alpha \]. After walking a distance d towards the foot of the tower the angle of elevation is found to be \[\beta \]. The height of the tower is:
(a) \[\dfrac{d}{\cot \alpha +\cot \beta }\]
(b) \[\dfrac{d}{\cot \alpha -\cot \beta }\]
(c) \[\dfrac{d}{\tan \beta -\tan \alpha }\]
(d) \[\dfrac{d}{\tan \beta +\tan \alpha }\]

Answer 1

Hint: First of all, draw a tower AB of height h and its angle of elevation at point of C on the ground. Now move distance ‘d’ towards the tower and draw an angle of elevation from the top of the tower at this point as \[\beta \]. Now take \[\tan \alpha \] and \[\tan \beta \] and use \[\tan \theta =\dfrac{perpendicular}{base}\] on two triangles to the desired required value.

Complete step-by-step answer:
Here, we are given that the angle of elevation of the top of a tower standing on a horizontal plane from a point A is \[\alpha \]. After walking a distance d towards the foot of the tower the angle of elevation is found to be \[\beta \]. We have to find the value of the height of the tower.
First of all, let us draw a tower AB and angle of its elevation as \[\alpha \].

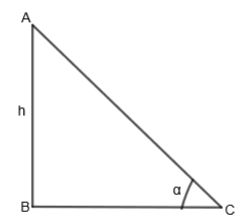
After walking a distance ‘d’ towards the tower, the angle of elevation is \[\beta \].

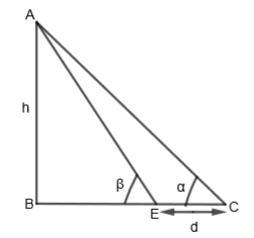
Let us assume that the height of the tower as h. Let us consider \[\Delta ABC\]. We know that,
\[\tan \theta =\dfrac{perpendicular}{base}\]
So, in \[\Delta ABC\], we get,
\[\tan \alpha =\dfrac{AB}{BC}....\left( i \right)\]
From the diagram, we can see that, AB =h, BC = BE + EC = BE + d
By substituting these values in equation (i), we get,
\[\tan \alpha =\dfrac{h}{BE+d}....\left( ii \right)\]
Now, let us consider \[\Delta ABE\], again we know that,
\[\tan \theta =\dfrac{perpendicular}{base}\]
So, in \[\Delta ABE\], we get,
\[\tan \beta =\dfrac{AB}{BE}\]
We know that AB = h, so we get,
\[\tan \beta =\dfrac{h}{BE}\]
By multiplying BE on both sides of the above equation, we get,
\[BE\tan \beta =h\]
\[\Rightarrow BE=\dfrac{h}{\tan \beta }\]
By substituting the value of BE in equation (ii), we get,
\[\tan \alpha =\dfrac{h}{\dfrac{h}{\tan \beta }+d}\]
By cross multiplying the above equation, we get,
\[\tan \alpha \left( \dfrac{h}{\tan \beta }+d \right)=h\]
\[\dfrac{\left( \tan \alpha \right)h}{\left( \tan \beta \right)}+\left( \tan \alpha \right)d=h\]
\[\left( \tan \alpha \right)d=h-h\left( \dfrac{\tan \alpha }{\tan \beta } \right)\]
By taking out h common, we get,
\[\left( \tan \alpha \right)d=h\left( 1-\dfrac{\tan \alpha }{\tan \beta } \right)\]
\[h=\dfrac{d\left( \tan \alpha \right)}{1-\dfrac{\tan \alpha }{\tan \beta }}\]
\[h=\dfrac{d\tan \alpha \tan \beta }{\left( \tan \beta -\tan \alpha \right)}\]
By dividing the numerator and denominator by \[\tan \alpha \tan \beta \], we get,
\[h=\dfrac{d}{\dfrac{\tan \beta -\tan \alpha }{\tan \alpha \tan \beta }}\]
\[h=\dfrac{d}{\dfrac{1}{\tan \alpha }-\dfrac{1}{\tan \beta }}\]
We know that \[\dfrac{1}{\tan \theta }=\cot \theta \]. By using this, we get,
\[h=\dfrac{d}{\cot \alpha -\cot \beta }\]
So, we get the height of the tower as \[\dfrac{d}{\cot \alpha -\cot \beta }\]
Hence, option (b) is the right answer.

Note: In this question, some students make this mistake of interchanging the position of \[\alpha \text{ and }\beta \]. So, this must be taken care of because a person is walking towards the tower and not away from it. Also, students must be careful while substituting \[\dfrac{h}{\tan \beta }\] in the expression of \[\tan \alpha \] because sometimes calculation mistakes arise.