
The angle of intersection between the curves
A.
B.
C.
D.
Answer
494.4k+ views
Hint: We need to find the angle of intersection between the curves
Complete step by step answer:
We need to find the angle of intersection between the curves
Let us find the range of
We know that the range of
And the range of
Therefore, range of
Now multiply and divide RHS by
Now,
Solving, we get
Therefore equation
We know that
Therefore,
Multiplying by
As
It is given that
Given that
Therefore, the intersection points are
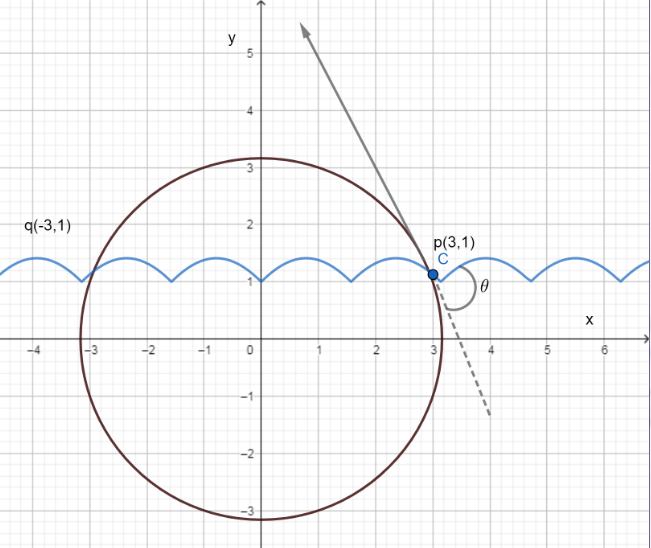
We need to find the slope of the tangent
Now differentiate
Now for the point
For the point
Therefore, slope
We have,
Differentiating
That is, the slope
Now, to find the angle of intersection, we have
We will use in this case
Substituting the value, we will get
Taking inverse of
Therefore,
Hence the correct options are A and B.
Note:
In this question, it is not necessary to write the steps to get the range of
We know that when
We know that at
So
Therefore, the maximum value of
To find the minimum value, we know that minimum value of
Now
Thus the range of
Complete step by step answer:
We need to find the angle of intersection between the curves
Let us find the range of
We know that the range of
And the range of
Therefore, range of
Now multiply and divide RHS by
Now,
Solving, we get
Therefore equation
We know that
Therefore,
Multiplying by
As
It is given that
Given that
Therefore, the intersection points are

We need to find the slope of the tangent
Now differentiate
Now for the point
For the point
Therefore, slope
We have,
Differentiating
That is, the slope
Now, to find the angle of intersection, we have
We will use in this case
Substituting the value, we will get
Taking inverse of
Therefore,
Hence the correct options are A and B.
Note:
In this question, it is not necessary to write the steps to get the range of
We know that when
We know that at
So
Therefore, the maximum value of
To find the minimum value, we know that minimum value of
Now
Thus the range of
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




